
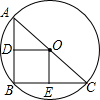
 如图,在⊙O中,AB,BC为互相垂直且相等的两条弦,连接AC.求证:
如图,在⊙O中,AB,BC为互相垂直且相等的两条弦,连接AC.求证:科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
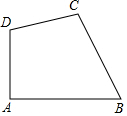 如图,四边形ABCD中,∠A=90°,AB=$5\sqrt{3}$,BC=8,CD=6,AD=5.
如图,四边形ABCD中,∠A=90°,AB=$5\sqrt{3}$,BC=8,CD=6,AD=5.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在一次数学活动课上,小明用18个棱长为1的正方体积木搭成一个几何体,然后他请小亮用其他棱长为1的正方体积木在旁边再搭一个几何体,使小亮所搭几何体恰好和小明所搭几何体拼成一个无空隙的大长方体(不改变小明所搭几何体的形状).
如图,在一次数学活动课上,小明用18个棱长为1的正方体积木搭成一个几何体,然后他请小亮用其他棱长为1的正方体积木在旁边再搭一个几何体,使小亮所搭几何体恰好和小明所搭几何体拼成一个无空隙的大长方体(不改变小明所搭几何体的形状).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
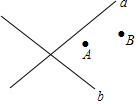 作图:A,B两村庄要建一个加油站,要求到A,B两村距离相等,且到公路a,b的距离也相等,请你帮忙确定加油站的位置P.(用直尺、圆规作图,保留作图痕迹)
作图:A,B两村庄要建一个加油站,要求到A,B两村距离相等,且到公路a,b的距离也相等,请你帮忙确定加油站的位置P.(用直尺、圆规作图,保留作图痕迹)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com