
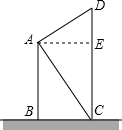
 小华家与小丽家的两楼相邻,且相距10米,如图,小华家的楼高AB为18米;从小华家楼的顶部目测小丽家住的楼房CD的底部与顶部,视线与水平线的夹角分别为55°和35°,你能否求出小丽家住的楼房CD有多高?请说明理由.
小华家与小丽家的两楼相邻,且相距10米,如图,小华家的楼高AB为18米;从小华家楼的顶部目测小丽家住的楼房CD的底部与顶部,视线与水平线的夹角分别为55°和35°,你能否求出小丽家住的楼房CD有多高?请说明理由. 分析 作AE⊥CD知四边形ABCE是矩形,可得AE=BC=10m、AB=CE=18m,证△DAE∽△ACE,根据$\frac{DE}{AE}$=$\frac{AE}{CE}$求得DE的长,进而可得CD.
解答 解:如图,作AE⊥CD于E,
∴∠AED=∠CEA=90°,
又∵AB⊥BC,DC⊥BC,
∴四边形ABCE是矩形,
∴AE=BC=10m,AB=CE=18m,
∵∠DAE=35°,∠CAE=55°,
∴∠D=∠CAE=55°,
∴△DAE∽△ACE,
∴$\frac{DE}{AE}$=$\frac{AE}{CE}$,即$\frac{DE}{10}$=$\frac{10}{18}$,
解得:DE=$\frac{50}{9}$,
则CD=CE+DE=18+$\frac{50}{9}$=$\frac{212}{9}$(m).
答:小丽家住的楼房CD有$\frac{212}{9}$米.
点评 本题主要考查相似三角形的判定与性质,构建相似的直角三角形求解是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
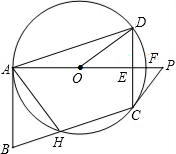 如图,⊙O过?ABCD的三顶点A、D、C,边AB与⊙O相切于点A,边BC与⊙O相交于点H,射线AP交边CD于点E,交⊙O于点F,点P在射线AO上,且∠PCD=2∠DAF.
如图,⊙O过?ABCD的三顶点A、D、C,边AB与⊙O相切于点A,边BC与⊙O相交于点H,射线AP交边CD于点E,交⊙O于点F,点P在射线AO上,且∠PCD=2∠DAF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com