
����Ŀ��ij�����۽�֮�磬������Ӵ���գ�ij������Ҫ��240�ֽ�������ij�е�A��B���أ��ô�С���ֻ�����20����ǡ����һ���������������ӣ���֪�����ֻ������������ֱ�Ϊ15��/����10��/����
��1�������ֻ������ж�������
��2������A�ص��˷�Ϊ����630Ԫ/����С��420Ԫ/��������B�ص��˷�Ϊ����750Ԫ/����С��550Ԫ/��������20�������е�10������ǰ��A�أ��������ǰ��B�أ����е���A�صĴ���a���������˷ѣ����ú�a��ʽ�ӱ�ʾ��
���𰸡���1��������Ϊ15��/���Ļ�����8����������Ϊ10��/���Ļ�����12������2�����˷ѣ�![]() ��Ԫ��.
��Ԫ��.
��������
��1����������Ϊ15��/���Ļ�����x����������Ϊ10��/���Ļ�����y�����������ֳ���20����һ�ο��˻���240�֣����ɵó�����x��y�Ķ�Ԫһ�η����飬��֮���ɵó����ۣ�
��2���ɵ���A�صĴ���a�����ɵó�����A�ص�С���У�10��a����������B�صĴ��У�8��a����������B�ص�С���У�2+a�������������˷ѣ�ÿ���������˷��������������ú�a��ʽ�ӱ�ʾ�����˷ѣ�
�⣺��1����������Ϊ15��/���Ļ�����x����������Ϊ10��/���Ļ�����y����
�����⣬�ã�![]() ��
��
��ã�![]() ��
��
��������Ϊ15��/���Ļ�����8����������Ϊ10��/���Ļ�����12����
��2���ߵ���A�صĴ���a����
�����A�ص�С���У�10��a����������B�صĴ��У�8��a����������B�ص�С���У�2+a������
�����˷�Ϊ630a+420��10��a��+750��8��a��+550��2+a����10a+11300��Ԫ����


 ������������Ӧ����ϵ�д�
������������Ӧ����ϵ�д� ͬ����չ�Ķ�ϵ�д�
ͬ����չ�Ķ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABC�ڽ���ԲO��I�ǡ�ABC�����ģ�AI���ӳ��߽�ԲO�ڵ�D��
��1����֤��BD=DI��
��2����OI��AD����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ھ���ABCD�У�E��CB�ӳ�����һ�����㣬F��G�ֱ�ΪAE��BC���е㣬FG��ED�ཻ�ڵ�H
(1) ��֤��HE��HG
(2) ��ͼ2����BE��ABʱ������A��AP��DE�ڵ�P����BP����![]() ��ֵ
��ֵ
(3) ��(2)�������£���AD��2����ADE��30�㣬��BP�ij�Ϊ______________


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��һ���ң�E��AB���е㣬����E��EC��OA�ڵ�C������B����O�����߽�CE���ӳ����ڵ�D�� 
��1����֤��DB=DE��
��2����AB=12��BD=5�����O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����BAC��ƽ���߽���ABC�����Բ�ڵ�D����ABC��ƽ���߽�AD�ڵ�E�� 
��1����֤��DE=DB��
��2������BAC=90�㣬BD=4�����ABC���Բ�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB�ǡ�O��ֱ������CD��ֱ��AB�ཻ�ڵ�F����E�ڡ�O�⣬��ֱ��AE���ҡ�EAC=��D 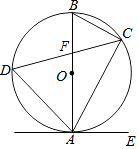
��1����֤��ֱ��AE�ǡ�O�����ߣ�
��2������BAC=30�㣬BC=4��cos��BAD= ![]() ��CF=
��CF= ![]() ����BF�ij���
����BF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��![]() ��
��![]() ������
������![]() .�����
.�����![]() ��ֱ��
��ֱ��![]() �ϣ��ҵ�
�ϣ��ҵ�![]() ��ֱ��
��ֱ��![]() �ľ��벻����1����ô�Ƶ�
�ľ��벻����1����ô�Ƶ�![]() ���߶�
���߶�![]() �ġ��ٽ��㡱.
�ġ��ٽ��㡱.

��1���жϵ�![]() �Ƿ����߶�
�Ƿ����߶�![]() �ġ��ٽ��㡱����˵�����ɣ�
�ġ��ٽ��㡱����˵�����ɣ�
��2������![]() ���߶�
���߶�![]() �ġ��ٽ��㡱.����
�ġ��ٽ��㡱.����![]() ��ȡֵ��Χ������ֱ��
��ȡֵ��Χ������ֱ��![]() ��
��![]() �ύ��
�ύ��![]() �㣬����
�㣬����![]() ����
����![]() �����
�����![]() �������
�������![]() ��������.
��������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
(1)��a3��a4��
(2) ![]() 2018��
2018��![]() 2019.
2019.
(3)(��2x2y)3��3(xy2)2��
(4)(��3a��2b)2
(5)(x��2)(x��2)(x2��4)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ABC=90�㣬��ACB=30�㣮����ABC�Ƶ�A����ʱ�뷽����ת15���õ���AB1C1 �� B1C1��AC�ڵ�D�����AD=2 ![]() �����ABC���ܳ����� ��
�����ABC���ܳ����� �� 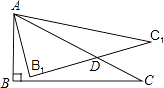
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com