
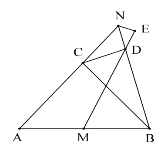
【题目】如图,△ABC 为等腰直角三角形,∠ACB=90°,点 M 为 AB 边的中点,点 N 为射线 AC 上一点,连接 BN,过点 C 作 CD⊥BN 于点 D,连接 MD,作∠BNE=∠BNA,边 EN 交射线 MD 于点 E,若 AB=20![]() ,MD=14
,MD=14![]() ,则 NE 的长为___.
,则 NE 的长为___.
【答案】![]()
【解析】
连接CM,过点M作MF⊥BD于F,根据等腰直角三角形的性质求出BM、BC,证出C、M、B、D四点共圆,根据圆周角定理的推论和等腰三角形的判定证出△DMF为等腰直角三角形,利用勾股定理和锐角三角函数求出BD和BN,然后证出△NDE∽△MDB列出比例式即可求出结论.
解:连接CM,过点M作MF⊥BD于F

∵△ABC 为等腰直角三角形,∠ACB=90°,点 M 为 AB 边的中点,AB=20![]() ,
,
∴BM=![]() AB=10
AB=10![]() ,AC=BC=20,∠CMB=90°,∠BCM=
,AC=BC=20,∠CMB=90°,∠BCM=![]() ∠ACB=45°
∠ACB=45°
∵CD⊥BN
∴∠CDB=90°
∴∠CDB+∠CMB=180°
∴C、M、B、D四点共圆
∴∠MDB=∠BCM=45°,∠DCB=∠BMD
∴△DMF为等腰直角三角形
∵MD=14![]() ,
,
∴MF=DF=14
在Rt△BMF中,BF=![]()
∴BD=BF+DF=16
∵cos∠CBN=![]()
即![]()
解得:BN=25
∴DN=BN-BD=9
∵∠BNE=∠BNA,而∠DCN+∠BNA=90°
∴∠BNE+∠DCN=90°
∵∠DCN+∠DCB=90°
∴∠BNE=∠DCB
∴∠BNE=∠BMD
∵∠NDE=∠MDB
∴△NDE∽△MDB
∴![]()
即![]()
解得:NE=![]()
故答案为:![]() .
.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】有两张完全重合的矩形纸片,将其中一张绕点![]() 顺时针旋转
顺时针旋转![]() 后得到矩形
后得到矩形![]() (如图1),连接
(如图1),连接![]() ,
,![]() ,若
,若![]() ,
,![]() .
.

(1)试探究线段![]() 与线段
与线段![]() 的数量关系和位置关系,并说明理由;
的数量关系和位置关系,并说明理由;
(2)把![]() 与
与![]() 剪去,将
剪去,将![]() 绕点
绕点![]() 顺时针旋转得
顺时针旋转得![]() ,边
,边![]() 交
交![]() 于点
于点![]() (如图2),设旋转角为
(如图2),设旋转角为![]() ,当
,当![]() 为等腰三角形时,求
为等腰三角形时,求![]() 的度数;
的度数;
(3)若将![]() 沿
沿![]() 方向平移得到
方向平移得到![]() (如图3),
(如图3),![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,当
,当![]() 时,求平移的距离.
时,求平移的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于二次函数![]() ,以下结论:①抛物线交
,以下结论:①抛物线交![]() 轴有两个不同的交点;②不论
轴有两个不同的交点;②不论![]() 取何值,抛物线总是经过一个定点;③设抛物线交
取何值,抛物线总是经过一个定点;③设抛物线交![]() 轴于
轴于![]() 、
、![]() 两点,若
两点,若![]() ,则
,则![]() ;④抛物线的顶点在
;④抛物线的顶点在![]() 图象上;⑤抛物线交
图象上;⑤抛物线交![]() 轴于
轴于![]() 点,若
点,若![]() 是等腰三角形,则
是等腰三角形,则![]() ,
,![]() ,
,![]() .其中正确的序号是( )
.其中正确的序号是( )
A. ①②⑤ B. ②③④ C. ①④⑤ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校随机对本校部分学生进行“假期中,我在家可以这么做:![]() .扎实学习、
.扎实学习、![]() .快乐游戏、
.快乐游戏、![]() .经典阅读、
.经典阅读、![]() .分担劳动、
.分担劳动、![]() .乐享健康”网络调查,并根据调查结果绘制成如下两幅不完整的统计图(若每一位同学只能选择一项),请根据图中信息,回答下列问题.
.乐享健康”网络调查,并根据调查结果绘制成如下两幅不完整的统计图(若每一位同学只能选择一项),请根据图中信息,回答下列问题.

(1)这次调查的总人数是___________人;
(2)请补全条形统计图,并说明扇形统计图中![]() 所对应的圆心角是___________度;
所对应的圆心角是___________度;
(3)若该学校共有学生1700人,则选择![]() 有多少人?
有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD与AB相交,连接CO,过点D作⊙O的切线,与AB的延长线交于点E,若DE∥AC,∠BAC=40°,则∠OCD的度数为( )
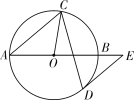
A.65°B.30°C.25°D.20°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为推动阳光体育运动的广泛开展,引导学生走向大自然,走到阳光下积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年级随机抽取了部分学生的鞋号,绘制了如图所示两个统计图,请根据相关信息,解答下列问题:
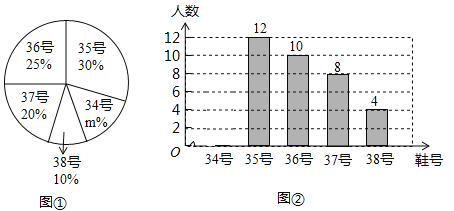
(1)求本次抽样调查的学生人数
(2)通过计算补全条形统计图和扇形统计图;
(3)若学生计划购买200双运动鞋,建议购买35号运动鞋约多少双?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com