

���� ��1������ƽ��������仯�Ĺ��ɿɵõ���C��D�����꣬Ȼ������ƽ�е����ʿɵõ�AC��BD��AC=BD�����ǿ��ж�ABCDΪƽ���ı��Σ�Ȼ������S�ı���ABDC=CO��AB������ı��ε������
��2��������ȷ�Ľ��ۣ�����P��PQ��CD������ƽ���߹����������ɵõ�PQ��AB��CD����ƽ���ߵ����ʺͽǵĺͲ��ϵ��֤����CPQ+��OPQ=��CPO���ʴ˿��������Ĵ𰸣�
��3���ٵ���P��x����ʱ���������ε������ʽ�����PB=8�����ǿɵõ�P�����ꣻ�ڵ���P��y����ʱ���������ε������ʽ�����PC=$\frac{16}{3}$�����ǿɵõ�P�����꣮
��� �⣺��1������ƽ�Ƶķ���;����֪����C��D������ֱ�ΪC��0��2����D��4��2����
����ƽ�Ƶ����ʿ�֪AC��BD��AC=BD��
��ABCDΪƽ���ı��Σ�
��S�ı���ABDC=CO��AB=2��4=8��
��2��������ȷ�Ľ��ۣ�
���ɣ���ͼ1��ʾ������P��PQ��CD��
��AB��CD��
��PQ��AB��CD��
���DCP=��CPQ����BOP=��OPQ��
���DCP+��BOP=��CPQ+��OPQ=��CPO��
��$\frac{��DCP+��BOP}{��CPO}$=$\frac{��CPD}{��CPO}$=1��
��3���ٵ���P��x����ʱ��
��S��PBC=$\frac{1}{2}$��PB��2=8��
��PB=8��
���P��-5��0����11��0����
�ڵ���P��y����ʱ��
��S��PBC=$\frac{1}{2}$��PC��3=8��
��PC=$\frac{16}{3}$��
���P��0��$\frac{22}{3}$����0��$-\frac{10}{3}$��
���������������ڵ�ΪP��-5��0����11��0����0��$\frac{22}{3}$����0��$-\frac{10}{3}$����
���� ������Ҫ������Ǽ��α任���ۺ�Ӧ�ã��������ҪӦ����ƽ�Ƶ����ʡ�ƽ���ı��ε��ж���ƽ���ߵ����ʡ������ε������ʽ��Ӧ�ã����������ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
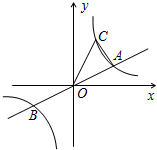 ��ͼ����ֱ֪��y=ax��˫����$y=\frac{k}{x}��k��0��$����A��B���㣬��B������ΪB��-2��-1����CΪ˫����$y=\frac{k}{x}��k��0��$��һ�㣬���ڵ�һ�����ڣ�
��ͼ����ֱ֪��y=ax��˫����$y=\frac{k}{x}��k��0��$����A��B���㣬��B������ΪB��-2��-1����CΪ˫����$y=\frac{k}{x}��k��0��$��һ�㣬���ڵ�һ�����ڣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ������ϵ�ڣ���֪��A��λ�ã���B��㣨-3��-1������ԭ��O�Գƣ�����A����ƽ��5����λ�����C��
��ͼ����ƽ��ֱ������ϵ�ڣ���֪��A��λ�ã���B��㣨-3��-1������ԭ��O�Գƣ�����A����ƽ��5����λ�����C���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a-��b+c�� | B�� | a-��b-c�� | C�� | a-��c-b�� | D�� | a+��b+c�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ����Rt��ABC�У���A=90�㣬BC�Ĵ�ֱƽ���߽�AB��E������ΪD������CE����CEƽ�֡�ACB�����B�Ķ���Ϊ30�㣮
��ͼ��ʾ����Rt��ABC�У���A=90�㣬BC�Ĵ�ֱƽ���߽�AB��E������ΪD������CE����CEƽ�֡�ACB�����B�Ķ���Ϊ30�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5��a��11 | B�� | 4��a��10 | C�� | -5��a��-2 | D�� | -2��a��-5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com