
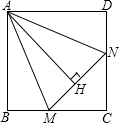
 已知,正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M、N,AH⊥MN于点H,如图MH=2,NH=3,求AH的长.
已知,正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M、N,AH⊥MN于点H,如图MH=2,NH=3,求AH的长. 分析 延长CB至E,使BE=DN,推出Rt△AEB≌Rt△AND,△AEM≌△ANM,得到AB=AH,根据全等三角形的性质得到BM=HM=2,同理DN=HN=3,根据勾股定理即可得到结论.
解答 解:延长CB至E,使BE=DN,
∵四边形ABCD是正方形,
∴AB=AD,∠D=∠ABE=90°,
在Rt△AEB和Rt△AND中,$\left\{\begin{array}{l}{AB=AD}\\{∠ABE=∠ADN}\\{BE=DN}\end{array}\right.$,
∴Rt△AEB≌Rt△AND,
∴AE=AN,∠EAB=∠NAD,
∴∠EAM=∠NAM=45°,
在△AEM和△ANM中,$\left\{\begin{array}{l}{AE=AN}\\{∠EAM=∠NAM}\\{AM=AM}\end{array}\right.$,
∴△AEM≌△ANM,
∴S△AEM=S△ANM,EM=MN,
∵AB、AH是△AEM和△ANM对应边上的高,
∴AB=AH,
∴AH=AB=BC=CD=AD,
在Rt△ABM与Rt△AHM中,$\left\{\begin{array}{l}{AB=AH}\\{AM=AM}\end{array}\right.$,
∴Rt△ABM≌Rt△AHM,
∴BM=HM=2,
同理DN=HN=3,
设AH=x,则MC=x-2,NC=x-3,
在Rt△MCN中,由勾股定理,得MN2=MC2+NC2,
∴52=(x-2)2+(x-3)2,
解得x1=6,x2=-1(不符合题意,舍去)
∴AH=6.
点评 本题考查了旋转的性质,正方形的性质,勾股定理,全等三角形的判定和性质,正确的作出辅助线是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
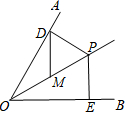 如图,已知OP平分∠AOB,∠AOB=60°,PE=2,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是( )
如图,已知OP平分∠AOB,∠AOB=60°,PE=2,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
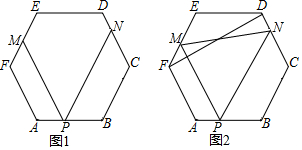 在正六边形ABCDEF中,P是AB边上一点,PM∥AF交EF于M,PN∥BC交CD于N.
在正六边形ABCDEF中,P是AB边上一点,PM∥AF交EF于M,PN∥BC交CD于N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
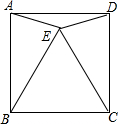 如图,在正方形ABCD中,△BCE是等边三角形,连接AE,DE.
如图,在正方形ABCD中,△BCE是等边三角形,连接AE,DE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{x+2}$=$\frac{4}{x+2}$ | B. | $\sqrt{x-2}$+x=0 | C. | x2-2=0 | D. | x2+y2=1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com