
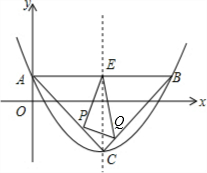
 以C(4,-2)为顶点的抛物线交y轴于点A(0,1),过点A平行于x轴的直线交抛物线于点B,交抛物线对称轴于点E.
以C(4,-2)为顶点的抛物线交y轴于点A(0,1),过点A平行于x轴的直线交抛物线于点B,交抛物线对称轴于点E.分析 (1)设顶点解析式为y=a(x-4)2-2,根据待定系数法可得抛物线解析式,进一步得到对称轴;
(2)①分PA=PE,AP=AE,EA=EP三种情况讨论可求当△APE为等腰三角形时t的值;
②分EP是∠AEQ的平分线,EQ是∠BEP的平分线两种情况讨论可求使得点E到三边AC,PQ,CB的距离相等时t的值.
解答 解:(1)设解析式为y=a(x-4)2-2,
代入得16a-2=1,
16a=3,
a=$\frac{3}{16}$.
解析式为$y=\frac{3}{16}{(x-4)^2}-2$,
对称轴为直线x=4;
(2)①PA=PE时,t=$\frac{5}{8}$,
AP=AE时,t=1,
EA=EP时,t=$\frac{8}{5}$;
②EP是∠AEQ的平分线时t=$\frac{5}{12}$,
EQ是∠BEP的平分线时t=3.
点评 考查了二次函数综合题,涉及的知识点有:待定系数法求函数解析式,二次函数的性质,等腰三角形的判定和性质,角平分线的性质,注意分类思想的应用.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:选择题
| A. | 兵兵 | B. | 芳芳 | C. | 婷婷 | D. | 杨辉 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
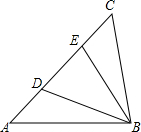 如图,已知△AEB≌△CDB,AE=DC,AB=BC,∠A=50°,∠AEB=70°,则∠CBD=( )
如图,已知△AEB≌△CDB,AE=DC,AB=BC,∠A=50°,∠AEB=70°,则∠CBD=( )| A. | 50° | B. | 60° | C. | 70° | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
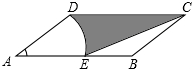 如图,在?ABCD中,BC=10,DC=12,∠B=150°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是55-$\frac{25}{3}$π(结果不取近似值)
如图,在?ABCD中,BC=10,DC=12,∠B=150°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是55-$\frac{25}{3}$π(结果不取近似值)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1≤y2 | B. | y1=y2 | C. | y1<y2 | D. | y1>y2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com