
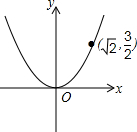 如图,已知二次函数y=ax2的图象经过点($\sqrt{2}$,$\frac{3}{2}$).
如图,已知二次函数y=ax2的图象经过点($\sqrt{2}$,$\frac{3}{2}$).分析 (1)利用待定系数法求得函数的解析式;
(2)在解析式中令y=3,求得x的值,则点的坐标即可求得;
(3)根据函数图象即可求解.
解答 解:(1)把($\sqrt{2}$,$\frac{3}{2}$)代入解析式得2a=$\frac{3}{2}$,
解得:a=$\frac{3}{4}$.
则抛物线的解析式是y=$\frac{3}{4}$x2;
(2)当y=3时,$\frac{3}{4}{x}^{2}$=3,
解得:x=2或-2,
则纵坐标是3的点是(-2,3)或(2,3),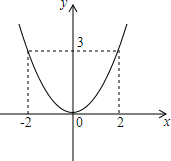 ;
;
(3)当-2<x<2时,y<3.
点评 本题考查了二次函数的图象与不等式,是一道设计精巧的数形结合题,数形结合是数学中的重要思想之一,解决函数问题更是如此,同学们要引起重视.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:解答题
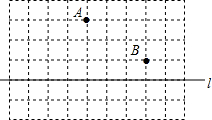 如图,是边长为1的小正方形组成的网格图,图中线与线的交点叫做格点.A、B都是格点,l是网格图中的一条直线.
如图,是边长为1的小正方形组成的网格图,图中线与线的交点叫做格点.A、B都是格点,l是网格图中的一条直线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
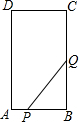 如图,在矩形ABCD中,AB=6cm,BC=10cm,点P从点A出发,沿AB边向点B以1cm/s的速度移动,同时点Q从点B出发沿BC边向点C以2cm/s的速度移动,如果P,Q两点同时出发,当一个点到达终点时,另一个点立即停止移动,点P运动时间为t秒.
如图,在矩形ABCD中,AB=6cm,BC=10cm,点P从点A出发,沿AB边向点B以1cm/s的速度移动,同时点Q从点B出发沿BC边向点C以2cm/s的速度移动,如果P,Q两点同时出发,当一个点到达终点时,另一个点立即停止移动,点P运动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
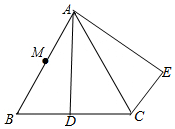 如图,△ABC是等边三角形,D是BC上一点,△ABD绕点A逆时针旋转到△ACE的位置.
如图,△ABC是等边三角形,D是BC上一点,△ABD绕点A逆时针旋转到△ACE的位置.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
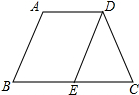 如图,在梯形ABCD中,AD∥BC,AB=DC,BC-AD=AB,过D作DE∥AB交BC于E,则△DEC是( )
如图,在梯形ABCD中,AD∥BC,AB=DC,BC-AD=AB,过D作DE∥AB交BC于E,则△DEC是( )| A. | 不等边三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com