
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=BC,点D是线段AB上的一点,连接CD,过点B作BG⊥CD,分别交CD,CA于点E,F,与过点A且垂直于AB的直线相交于点G,连接DF.给出以下四个结论:①![]() ②若点D是AB的中点,则AF=
②若点D是AB的中点,则AF=![]() AB;③当B,C,F,D四点在同一个圆上时,DF=DB;④若
AB;③当B,C,F,D四点在同一个圆上时,DF=DB;④若![]() ,则
,则![]() ,其中正确的结论序号是( )
,其中正确的结论序号是( )

A. ①② B. ③④ C. ①②③ D. ①②③④
【答案】C
【解析】解:∵∠ABC=90°,∠GAD=90°,∴AG∥BC,∴△AFG∽△CFB,∴ ![]() .∵BC=AB,∴
.∵BC=AB,∴![]() ,∴①正确.
,∴①正确.
∵∠BCD+∠EBC=∠EBC+∠ABG=90°,∴∠BCD=∠ABG.∵AB=BC,∠GAB=∠DBC=90°,∴△CBD≌△BAG,∴AG=BD.∵BD=![]() AB,∴
AB,∴![]() ,∴
,∴![]() ,∴
,∴![]() .∵AC=
.∵AC=![]() AB,∴AF=
AB,∴AF=![]() AB,∴②正确;
AB,∴②正确;
∵B,C,F,D四点共圆,∠DBC=90°,∴CD为直径,∴∠CFD=90°.∵BF⊥CD,∴BE=EF,∴BD=DE,∴③正确;
∵AG∥BC,∴ ![]() .∵BC=AB,∴
.∵BC=AB,∴![]() .∵AG=BD,
.∵AG=BD, ![]() ,∴
,∴![]() ,∴
,∴![]() =
=![]() ,∴AF=
,∴AF=![]() AC,∴S△ABF=
AC,∴S△ABF=![]() S△ABC,∴S△BDF=
S△ABC,∴S△BDF=![]() S△ABF,∴S△BDF=
S△ABF,∴S△BDF=![]() S△ABC,即S△ABC=12S△BDF,∴④错误.
S△ABC,即S△ABC=12S△BDF,∴④错误.
故答案为:①②③.


科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,直径AB垂直于弦CD,垂足为E,连结AC,将△ACE沿AC翻转得到△ACF,直线FC与直线AB相交于点G.
(1)求证:FG是⊙O的切线;
(2)若B为OG的中点,CE=![]() ,求⊙O的半径长;
,求⊙O的半径长;
(3)①求证:∠CAG=∠BCG;
②若⊙O的面积为4π,GC=2![]() ,求GB的长.
,求GB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】己知图甲是一个长为2m、宽为2n的长方形,沿图甲中虚线用剪刀均匀分成四小块长方形,然后按图乙的形状拼成一个正方形.

(1)图乙中阴影部分正方形的边长为________(用含字母m,n的整式表示).
(2)请用两种不同的方法求图乙中阴影部分的面积.
方法一:________________;
方法二:________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个四棱柱,
(1)若它的底面边长都是5cm,所有侧面的面积和是40cm,那么它的侧棱长是多少?
(2)若它的所有棱都相等,且所有棱长之和为60cm,那么它的形状是什么?它的体积是多少?
(3)若它的底面是等腰梯形,上下底边长分别为2cm,8cm,腰长为5cm,高是4cm,它的侧棱长是底面周长的一半,求该四棱柱的体积.
查看答案和解析>>
科目:初中数学 来源: 题型:
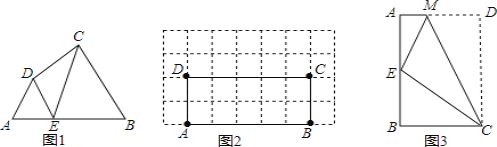
【题目】阅读理解:如图1,在四边形ABCD的边AB上任取一点E(点E不与点A、点B重合),分别连接ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点.解决问题:
(1)如图1,∠A=∠B=∠DEC=55°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图2,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图2中画出矩形ABCD的边AB上的一个强相似点E;
拓展探究:
(3)如图3,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处.若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB和BC的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
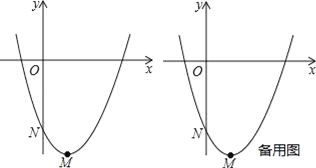
【题目】已知抛物线l:y=ax2+bx+c(a,b,c均不为0)的顶点为M,与y轴的交点为N,我们称以N为顶点,对称轴是y轴且过点M的抛物线为抛物线l的衍生抛物线,直线MN为抛物线l的衍生直线.
(1)如图,抛物线y=x2﹣2x﹣3的衍生抛物线的解析式是 ,衍生直线的解析式是 ;
(2)若一条抛物线的衍生抛物线和衍生直线分别是y=﹣2x2+1和y=﹣2x+1,求这条抛物线的解析式;
(3)如图,设(1)中的抛物线y=x2﹣2x﹣3的顶点为M,与y轴交点为N,将它的衍生直线MN先绕点N旋转到与x轴平行,再沿y轴向上平移1个单位得直线n,P是直线n上的动点,是否存在点P,使△POM为直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,以对角线BD为一边构造一个矩形BDEF,使得另一边EF过原矩形的顶点C.
(1)设Rt△CBD的面积为S1,Rt△BFC的面积为S2,Rt△DCE的面积为S3,则S1__ __S2+S3;(填“>”“=”或“<”)
(2)写出图中的三对相似三角形,并选择其中一对进行证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017山东德州第21题)如图所示,某公路检测中心在一事故多发地带安装了一个测速仪,检测点设在距离公路10m的A处,测得一辆汽车从B处行驶到C处所用的时间为0.9秒.已知∠B=30°,∠C=45°
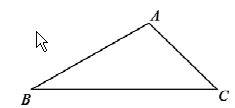
(1)求B,C之间的距离;(保留根号)
(2)如果此地限速为80km/h,那么这辆汽车是否超速?请说明理由.(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.

(1)求证:四边形DEFG是平行四边形;
(2)若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com