
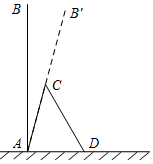
 一棵大树AB(假定大树AB垂直于地面)被刮倾斜15°后折断在地上,树的顶部恰好接触到地面D处(如示意图所示),量得大树的倾斜角∠BAC=15°,大树被折断部分和地面所成的角∠ADC=60°,AD=4米,求大树AB原来的高度是多少米?(结果保留整数,参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,$\sqrt{6}$≈2.4)
一棵大树AB(假定大树AB垂直于地面)被刮倾斜15°后折断在地上,树的顶部恰好接触到地面D处(如示意图所示),量得大树的倾斜角∠BAC=15°,大树被折断部分和地面所成的角∠ADC=60°,AD=4米,求大树AB原来的高度是多少米?(结果保留整数,参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,$\sqrt{6}$≈2.4) 分析 过点A作AE⊥CD于点E,先由直角三角形的性质求出∠DAC与∠DAE的度数,再由锐角三角函数的定义求出AE及DE的长,在Rt△ACE中,根据AC=$\frac{CE}{sin45°}$即可得出结论.
解答 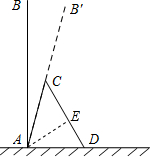 解:如图,过点A作AE⊥CD于点E,
解:如图,过点A作AE⊥CD于点E,
∵∠BAD=90°,∠BAC=15°
∴∠DAC=∠BAD-∠BAC=75°,
∵∠ADC=60°,∠AED=90°,
∴∠DAE=90°-∠ADC=30°.
在Rt△ADE中,AE=AD•sin60°=2$\sqrt{3}$,
DE=AD•cos60°=4•cos60°=2.
在Rt△ACE中,
∵∠CAE=∠DAC-∠DAE=45°,
∴CE=AE•tan45°=2$\sqrt{3}$,
∴AC=$\frac{CE}{sin45°}$=2$\sqrt{6}$,
AB=AC+CE+DE=2$\sqrt{6}$+2$\sqrt{3}$+2≈10(米),
即大树AB原来的高度约为10米.
点评 本题考查的是解直角三角形的应用,根据题意作出辅助线,构造出直角三角形是解答此题的关键.


 星级口算天天练系列答案
星级口算天天练系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
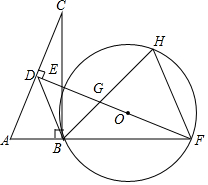 如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F,且BF=BC.⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交⊙O于点H,连接BD,FH.
如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F,且BF=BC.⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交⊙O于点H,连接BD,FH.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
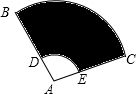 如图,扇形纸扇完全打开后,外侧两竹条AB、AC夹角为120°,AB的长为30cm,无贴纸部分AD的长为10cm,则贴纸部分的面积等于$\frac{800}{3}$πcm2.
如图,扇形纸扇完全打开后,外侧两竹条AB、AC夹角为120°,AB的长为30cm,无贴纸部分AD的长为10cm,则贴纸部分的面积等于$\frac{800}{3}$πcm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
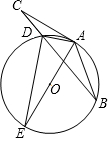 如图,在△ABC中,点D为BC上一点,过A,B,D三点作⊙O,AE是⊙O的直径,AC是⊙O的切线,AD=DC,连结DE.
如图,在△ABC中,点D为BC上一点,过A,B,D三点作⊙O,AE是⊙O的直径,AC是⊙O的切线,AD=DC,连结DE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com