
【题目】 如图,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点D是直线AB上一动点(不包含点A,B),过点B作BE⊥CD于点E,连接EA.
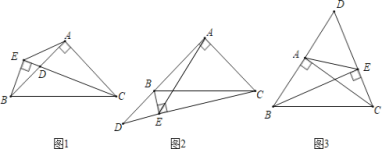
(1)如图1,当点D在线段AB上时,直接写出线段CE,BE,AE的数量关系:______.
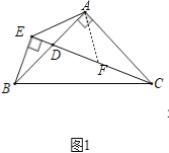
(2)如图2,当点D在线段AB的延长线上时,判断线段CE,BE,AE的数量关系,并加以证明.
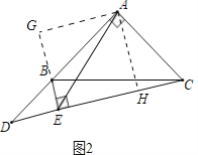
(3)如图3,当点D在线段BA的延长线上时,并将已知条件中的“AB=AC”改成;![]() ,其他条件不变,若CE=1,
,其他条件不变,若CE=1,![]() ,请直接写出线段BE的长.
,请直接写出线段BE的长.
【答案】(1)![]() ;(2)
;(2)![]() ,证明见解析;(3)
,证明见解析;(3)![]()
【解析】
(1)作AF⊥AE交CE于F.证明△EAB≌△FAC(AAS),然后得出△AEF是等腰直角三角形,即可解决问题;
(2)作AH⊥CD于H,AG⊥EB于G.先证明∠AEB=∠AEC,根据角平分线的性质得出AG=AH,即可根据HL得出Rt△AGB≌Rt△AHC,然后得出△AEF是等腰直角三角形,从而可解决问题;
(3)作AF⊥AE交BE于F.先证明∠AEF=∠ACB=30°,有![]() =
=![]() ,从而可得出△BAF∽△CAE,再利用相似三角形的性质以及勾股定理即可解决问题.
,从而可得出△BAF∽△CAE,再利用相似三角形的性质以及勾股定理即可解决问题.
解:(1)结论:![]() .
.
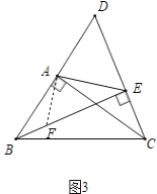
理由如下:如图1中,作AF⊥AE交CE于F.
∵BE⊥EC,
∴∠BED=∠CAD=90°,
∵∠EDB=∠ADC,
∴∠EBD=∠ACD,
∵∠EAF=∠BAC=90°,
∴∠EAB=∠CAF,
∵AB=AC,
∴△EAB≌△FAC(AAS),
∴BE=CF,AE=AF,
∴△AEF是等腰直角三角形,
∴EF=![]() AE,
AE,
∴EC-CF=EC-BE=EF=![]() AE,
AE,
∴EC-BE=![]() AE.
AE.
故答案为:EC-BE=![]() AE.
AE.
(2)如图2中,结论:![]() .
.
理由如下:作AH⊥CD于H,AG⊥EB于G.
∵∠BEC=∠BAC=90°,
∴∠BAC+∠CEB=180°,
∴A,B,E,C四点共圆,
∴∠AEC=∠ABC=45°,∠AEB=∠ACB=45°,
∴∠AEB=∠AEC,
∵AH⊥EC,AG⊥GE,
∴AG=AH,
∵AB=AC,∠AGB=∠AHC=90°,
∴Rt△AGB≌Rt△AHC(HL),
∴BG=CH,
∵∠AEH=∠EAH=∠AEG=∠EAG=45°,
∴AG=EG=AH=EH,∴AE=![]() EH,
EH,
∴EC+EB=EH+CH+EG-GB=2EH=![]() AE.
AE.
即BE+EC=![]() AE.
AE.
(3)如图3中,作AF⊥AE交BE于F.
在Rt△ABC中,∵tan∠ABC=![]() =
=![]() ,
,
∴∠ABC=60°,∠ACB=30°,
∵∠BAC=∠BEC=90°,
∴A,B,C,E四点共圆,
∴∠AEF=∠ACB=30°,
∴AE=![]() AF,
AF,
∴![]() =
=![]() ,
,
∵∠BAC=∠EAF=90°,
∴∠BAF=∠CAE,
∴△BAF∽△CAE,
∴![]() =
=![]() =
=![]() ,
,
∴BF=![]() EC=
EC=![]() ,
,
∵AE=![]() ,
,
∴AF=1,
∴EF=![]() =2,
=2,
∴![]() .
.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案科目:初中数学 来源: 题型:
【题目】问题探究:
(1)如图①所示是一个半径为![]() ,高为4的圆柱体和它的侧面展开图,AB是圆柱的一条母线,一只蚂蚁从A点出发沿圆柱的侧面爬行一周到达B点,求蚂蚁爬行的最短路程.(探究思路:将圆柱的侧面沿母线AB剪开,它的侧面展开图如图①中的矩形
,高为4的圆柱体和它的侧面展开图,AB是圆柱的一条母线,一只蚂蚁从A点出发沿圆柱的侧面爬行一周到达B点,求蚂蚁爬行的最短路程.(探究思路:将圆柱的侧面沿母线AB剪开,它的侧面展开图如图①中的矩形![]() 则蚂蚁爬行的最短路程即为线段
则蚂蚁爬行的最短路程即为线段![]() 的长)
的长)

(2)如图②所示是一个底面半径为![]() ,母线长为4的圆锥和它的侧面展开图,PA是它的一条母线,一只蚂蚁从A点出发沿圆锥的侧面爬行一周后回到A点,求蚂蚁爬行的最短路程.
,母线长为4的圆锥和它的侧面展开图,PA是它的一条母线,一只蚂蚁从A点出发沿圆锥的侧面爬行一周后回到A点,求蚂蚁爬行的最短路程.
(3)如图③所示,在②的条件下,一只蚂蚁从A点出发沿圆锥的侧面爬行一周到达母线PA上的一点,求蚂蚁爬行的最短路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
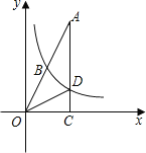
【题目】如图,已知在Rt△OAC中,∠OCA=90°,O为坐标原点,直角顶点C在x轴的正半轴上,反比例函数y=![]() (k>0)在第一象限的图象经过OA的中点B,交AC于点D,连接OD.若∠A=∠COD,则直线OA的解析式为______.
(k>0)在第一象限的图象经过OA的中点B,交AC于点D,连接OD.若∠A=∠COD,则直线OA的解析式为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料
计算:(1﹣![]() ﹣
﹣![]() )×(
)×(![]() +
+![]() )﹣(1﹣
)﹣(1﹣![]() ﹣
﹣![]() )(
)(![]() +
+![]() ),令
),令![]() +
+![]() =t,则:
=t,则:
原式=(1﹣t)(t+![]() )﹣(1﹣t﹣
)﹣(1﹣t﹣![]() )t=t+
)t=t+![]() ﹣t2﹣
﹣t2﹣![]() +t2=
+t2=![]()
在上面的问题中,用一个字母代表式子中的某一部分,能达到简化计算的目的,这种思想方法叫做“换元法”,请用“换元法”解决下列问题:
(1)计算:(1﹣![]() ﹣
﹣![]() )×(
)×(![]() +
+![]() )﹣(1﹣
)﹣(1﹣![]() ﹣
﹣![]() )×(
)×(![]() +
+![]() )
)
(2)因式分解:(a2﹣5a+3)(a2﹣5a+7)+4
(3)解方程:(x2+4x+1)(x2+4x+3)=3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查.调查结果显示,支付方式有:A微信、B支付宝、C现金、D其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.
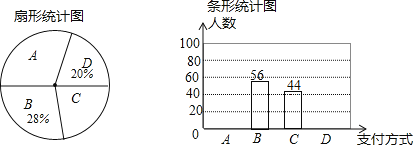
请你根据统计图提供的信息,解答下列问题:
(1)本次一共调查了多少名购买者?
(2)请补全条形统计图;在扇形统计图中A种支付方式所对应的圆心角为 度.
(3)若该超市这一周内有1600名购买者,请你估计使用A和B两种支付方式的购买者共有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD是矩形,过点D作DF∥AC交BA的延长线于点F.
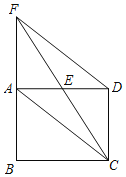
(1)求证:四边形ACDF是平行四边形;
(2)若AB=3,DF=5,求△AEC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是长沙九龙仓国际金融中心,位于长沙市黄兴路与解放路交会处的东北角,投资160亿元人民币,总建筑面积达98万平方米,中心主楼BC高452m,是目前湖南省第一高楼,大楼顶部有一发射塔AB,已知和BC处于同一水平面上有一高楼DE,在楼DE底端D点测得A的仰角为α,tanα=![]() ,在顶端E点测得A的仰角为45°,AE=140
,在顶端E点测得A的仰角为45°,AE=140![]() m
m
(1)求两楼之间的距离CD;
(2)求发射塔AB的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一座圆弧形拱桥,桥下水面宽度AB为12m,拱高CD为4m.
(1)求拱桥的半径;
(2)有一艘宽5m的货船,船舱顶部为长方形,并高出水面3.6m,求此货船是否能顺利通过拱桥?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市今年 1 月份的销售额为 500 万元,超市预计每个月的销售额会逐月增加.预测 3 月 份的销售额比 2 月份增加 120 万元;
(1)求 2、3 月份平均每月销售额的增长率;
(2)按照这样的增长速度,超市想在第一季度完成 1800 万元的销售目标是否能实现?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com