
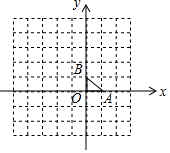
 �������P�ƶ���M��ת180������Q�غϣ���ô�Ƶ�P���Q���ڵ�M�Գƣ�����M�����Գ����ģ���ʱ��M���߶�PQ���е㣮��ͼ����ֱ������ϵ�У���ABO�Ķ���A��B��O������ֱ�Ϊ��1��0������0��1������0��0��������P1��P2��P3���е��������㶼���ڡ�ABO��һ������Գƣ���P1���P2���ڵ�A�Գƣ���P2���P3���ڵ�B�Գƣ���P3���P4���ڵ�O�Գƣ���P4���P5���ڵ�A�Գƣ���P5���P6���ڵ�B�Գƣ���P6���P7���ڵ�O�Գơ��Գ����ķֱ���A��B��O��A��B��O����������Щ�Գ���������ѭ������֪��P1�������ǣ�1��1������P2�������ǣ�1��-1����P2014�������ǣ�1��-3����
�������P�ƶ���M��ת180������Q�غϣ���ô�Ƶ�P���Q���ڵ�M�Գƣ�����M�����Գ����ģ���ʱ��M���߶�PQ���е㣮��ͼ����ֱ������ϵ�У���ABO�Ķ���A��B��O������ֱ�Ϊ��1��0������0��1������0��0��������P1��P2��P3���е��������㶼���ڡ�ABO��һ������Գƣ���P1���P2���ڵ�A�Գƣ���P2���P3���ڵ�B�Գƣ���P3���P4���ڵ�O�Գƣ���P4���P5���ڵ�A�Գƣ���P5���P6���ڵ�B�Գƣ���P6���P7���ڵ�O�Գơ��Գ����ķֱ���A��B��O��A��B��O����������Щ�Գ���������ѭ������֪��P1�������ǣ�1��1������P2�������ǣ�1��-1����P2014�������ǣ�1��-3���� ���� �����öԳ����ĵĶ���ֱ�ȷ��P1��P2��P3��P4��P5��P6��P7�����꣬���ֵ�P7������͵�P1��������ͬ������Щ���������6��Ϊһ�����ѭ�����ɴ˿�ȷ����P2014������͵�P4��������ͬ��
��� �⣺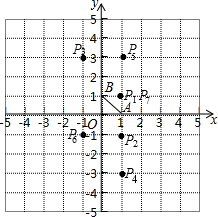 �ߵ�P1�������ǣ�1��1����A��1��0����
�ߵ�P1�������ǣ�1��1����A��1��0����
����P1���P2���ڵ�A�Գƣ�
���P2��������1��-1����
ͬ���õ���P3������Ϊ��-1��3����
��P4��������1��-3����
��P5����������1��3����
��P6��������-1��-1����
��P7������Ϊ��1��1������ͼ��
���P7������͵�P1��������ͬ��
��2014=335��6+4��
���P2014������͵�P4��������ͬ����Ϊ��1��-3����
�ʴ��ǣ���1��-1������1��-3����
���� ���⿼����������ͼ�α仯-��ת��ͼ�λ����ת֮��Ҫ�����ת�ĽǶȺ�ͼ�ε����������������ת��ĵ�����꣮����������ת����Ƕ��磺30�㣬45�㣬60�㣬90�㣬180�㣮ע��������������ҹ��ɣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2a | B�� | 2b | C�� | 2a+2b | D�� | 2b-2c |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com