
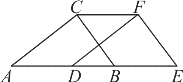
【题目】如图,在直角三角形ABC中,∠ACB=90°,AC=4cm,BC=3cm,将三角形ABC沿AB方向向右平移得到三角形DEF,若AE=8cm,DB=2cm.
(1)求三角形ABC向右平移的距离AD的长;
(2)求四边形AEFC的周长.
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】在每个小正方形的边长为 ![]() 的网格图形中,每个小正方形的顶点称为格点.从一个格点移动到与之相距
的网格图形中,每个小正方形的顶点称为格点.从一个格点移动到与之相距 ![]() 的另一个格点的运动称为一次跳马变换.例如,在
的另一个格点的运动称为一次跳马变换.例如,在 ![]() 的正方形网格图形中(如图1),从点
的正方形网格图形中(如图1),从点 ![]() 经过一次跳马变换可以到达点
经过一次跳马变换可以到达点 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 等处.现有
等处.现有 ![]() 的正方形网格图形(如图2),则从该正方形的顶点
的正方形网格图形(如图2),则从该正方形的顶点 ![]() 经过跳马变换到达与其相对的顶点
经过跳马变换到达与其相对的顶点 ![]() ,最少需要跳马变换的次数是( )
,最少需要跳马变换的次数是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,所有小正方形的边长都为1,A、B、C都在格点上.
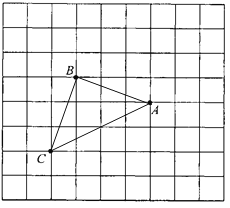
(1)过点B画直线AC的垂线,并注明垂足为G;
(2)线段 的长度是点B到直线AC的距离;
线段BC的长度是点 到直线 的距离;
(3)因为直线外一点与直线上各点连接的所有线段中,垂线段最短,所以线段BC、BG的大小关系为:BC BG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】金秋十月,长沙市某中学组织七年级学生去某综合实践基地进行秋季社会实践活动,每人需购买一张门票,该综合实践基地的门票价格为每张240元,如果一次购买500张以上(不含500张)门票,则门票价格为每张220元,请回答下列问题:
(1)列式表示n个人参加秋季社会实践活动所需钱数;
(2)某校用132000元可以购买多少张门票;
(3)如果我校490人参加秋季社会实践,怎样购买门票花钱最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课题学习:设计概率模拟实验. 在学习概率时,老师说:“掷一枚质地均匀的硬币,大量重复实验后,正面朝上的概率约是 ![]() .”小海、小东、小英分别设计了下列三个模拟实验:
.”小海、小东、小英分别设计了下列三个模拟实验:
小海找来一个啤酒瓶盖(如图1)进行大量重复抛掷,然后计算瓶盖口朝上的次数与总次数的比值;
小东用硬纸片做了一个圆形转盘,转盘上分成8个大小一样的扇形区域,并依次标上1至8个数字(如图2),转动转盘10次,然后计算指针落在奇数区域的次数与总次数的比值;
小英在一个不透明的盒子里放了四枚除颜色外都相同的围棋子(如图3),其中有三枚是白子,一枚是黑子,从中随机同时摸出两枚棋子,并大量重复上述实验,然后计算摸出的两枚棋子颜色不同的次数与总次数的比值.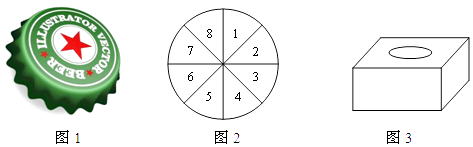
根据以上材料回答问题:
小海、小东、小英三人中,哪一位同学的实验设计比较合理,并简要说出其他两位同学实验的不足之处.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(-5a4)·(-8ab2)=_______;
(2)(-![]() x2yz2)2·(3xy2)2=_______;
x2yz2)2·(3xy2)2=_______;
(3)a(2-a)-2(a+1)=________;
(4)(4x2-3x+6)·(-![]() x)=_______;
x)=_______;
(5)3x2y·(![]() x3y2)·(5xy2)=________
x3y2)·(5xy2)=________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M沿路线O→A→C运动.
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)当△OMC的面积是△OAC的面积的![]() 时,求出这时点M的坐标.
时,求出这时点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有四张背面完全相同的纸牌A、B、C、D,其正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀.
(1)从中随机摸出一张,求摸出的牌面图形是中心对称图形的概率;
(2)小明和小亮约定做一个游戏,其规则为:先由小明随机摸出一张纸牌,不放回,再由小亮从剩下的纸牌中随机摸出一张,若摸出的两张牌面图形都是轴对称图形小明获胜,否则小亮获胜,这个游戏公平吗?请用列表法(或树状图)说明理由(纸牌用A、B、C、D表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,AB是⊙O的直径,点P在CA的延长线上,∠CAD=45°.
(Ⅰ)若AB=4,求 ![]() 的长;
的长;
(Ⅱ)若 ![]() =
= ![]() ,AD=AP,求证:PD是⊙O的切线.
,AD=AP,求证:PD是⊙O的切线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com