
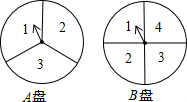
 下面是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,并分别标记了数字1,2,3和1,2,3,4.小明和小亮利用这两个转盘做游戏.规则如下:同时转动两个转盘,指针停止后,将指针所指区域的数字相加(若指针停在分界线上,则重新转动转盘),如果和为奇数,则小明获胜,如果和是偶数,则小亮获胜,请你确定游戏规则是否公平,并说明理由.
下面是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,并分别标记了数字1,2,3和1,2,3,4.小明和小亮利用这两个转盘做游戏.规则如下:同时转动两个转盘,指针停止后,将指针所指区域的数字相加(若指针停在分界线上,则重新转动转盘),如果和为奇数,则小明获胜,如果和是偶数,则小亮获胜,请你确定游戏规则是否公平,并说明理由. 分析 首先根据题意画出树状图,然后由树状图求得所有等可能的结果与数字之和为奇数和偶数的情况,再利用概率公式求出小明和小亮获胜的概率,然后进行比较,即可得出答案.
解答 解:根据题意画树状图如下: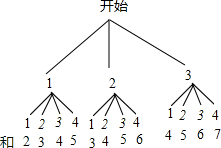
∵共有12种等可能的结果,和为奇数的有6种情况,和为偶数有6种情况,
∴P(小明获胜):$\frac{6}{12}$=$\frac{1}{2}$;
P(小亮获胜):$\frac{6}{12}$=$\frac{1}{2}$;
∴P(小明获胜)=P(小亮获胜),
∴这个游戏规则对小明、小亮双方公平.
点评 本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
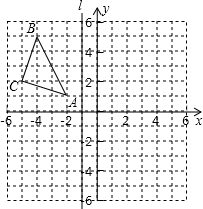 如图,△ABC在平面直角坐标系中,点A、B、C的坐标分别为A(-2,1),B(-4,5),C(-5,2),直线l经过点(-1,0)且和y轴平行.
如图,△ABC在平面直角坐标系中,点A、B、C的坐标分别为A(-2,1),B(-4,5),C(-5,2),直线l经过点(-1,0)且和y轴平行.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
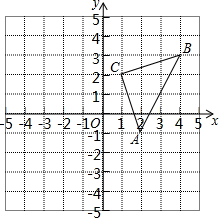 如图,平面直角坐标系中,△ABC的顶点都在网格点上,平移△ABC,使点B与坐标原点O重合,请在图中画出平移后的三角形A1OC1,并写出A1,C1的坐标.
如图,平面直角坐标系中,△ABC的顶点都在网格点上,平移△ABC,使点B与坐标原点O重合,请在图中画出平移后的三角形A1OC1,并写出A1,C1的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com