【题目】已知：BD为
的直径，O为圆心，点A为圆上一点，过点B作的切线交DA的延长线于点F，点C为上一点，且
，连接BC交AD于点E，连接AC．
如图1，求证：
；
如图2，点H为内部一点，连接OH，CH若
时，求证：
；
在的条件下，若
，的半径为10，求CE的长．
阶梯计算系列答案科目：初中数学 来源： 题型：
【题目】如图，∠AOB＝30，∠AOB内有一定点P，且OP＝10．在OA上有一动点Q，OB上有一动点R．若ΔPQR周长最小，则最小周长是___________
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小烨在探究数轴上两点间距离时发现：若
两点在
轴上或与轴平行，两点的横坐标分别为
，则两点间距离为
；若两点在
轴上或与轴平行，两点的纵坐标分别为
，则两点间距离为
.据此，小烨猜想：对于平面内任意两点
，
两点间的距离为
.
（1）请你利用下图，试证明：；
（2）若
，试在轴上求一点
，使
的距离最短，并求出的最小值和点坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某工程队用甲、乙两台隧道挖掘机从两个方向挖掘同一条隧道，因为地质条件不同，甲、乙的挖掘速度不同，已知甲、乙同时挖掘
天，可以挖
米，若甲挖
天，乙挖
天可以挖掘
米．
（1）请问甲、乙挖掘机每天可以挖掘多少米？
（2）若乙挖掘机比甲挖掘每小时多挖掘
米，甲、乙每天挖掘的时间相同，求甲每小时挖掘多少米？
（3）若隧道的总长为
米，甲、乙挖掘机工作
天后，因为甲挖掘机进行设备更新，乙挖掘机设备老化，甲比原来每天多挖
米，同时乙比原来少挖米
．最终，甲、乙两台挖掘机在相同时间里各完成隧道总长的一半，请用含，的代数式表示．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在8×8的正方形网格中，每个小正方形的边长都为1，网格中有一个格点△ABC（即三角形的顶点都在格点上）.
（1）在图中作出△ABC关于直线l对称的△A1B1C1；（要求：A与A1，B与B1，C与C1相对应）
（2）
是 三角形；
（3）若有一格点P到点A、B的距离相等（PA=PB），则网格中满足条件的点P共有 个；
(4)在直线
上找一点Q，使QB+QC的值最小。
查看答案和解析>>
科目：初中数学 来源： 题型：
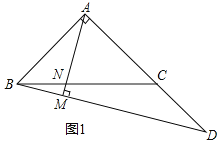
【题目】如图，在
中，
，点D为AC延长线上一点，连接BD，过A作
，垂足为M，交BC于点N
如图1，若
，
，求AM的长；
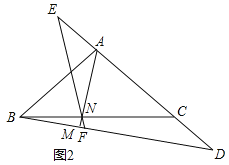
如图2，点E在CA的延长线上，且
，连接EN并延长交BD于点F，求证：
；
在的条件下，当
时，请求出
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
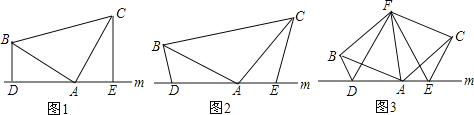
【题目】(1)如图1，已知：在△ABC中，∠BAC=90°，AB=AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E．猜测DE、BD、CE三条线段之间的数量关系(直接写出结果即可)．
(2)如图2，将(1)中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上，并且有∠BDA=∠AEC=∠BAC=α，其中α为任意锐角或钝角．请问第(1)题中DE、BD、CE之间的关系是否仍然成立？如成立，请你给出证明；若不成立，请说明理由．
(3)拓展与应用：如图3，D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合)，点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD、CE，若∠BDA=∠AEC=∠BAC，试判断线段DF、EF的数量关系，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知在图一中，将等边
绕BC边中点D顺时针旋转
至
，直线AG与直线CF交于点
求证
．小明同学的思路是这样的：通过证明
∽
得到
，从而得到
，继续推理就可以使问题得到解决．
请根据小明的思路，求证：；
爱动脑筋的小明把问题做了进一步思考，他想：如果把题目的“等边”改成“等腰直角，其中
，
”，如图二，中的结论还成立吗？如果成立，求此时线段BM的最大值．
小明继续大胆设问：如图三，在中，
，
，将这样的按照题目中的方式旋转，请直接写出AG与CF的位置关系以及线段BM的变化范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在课外活动时间，甲、乙、丙做“互相踢毽子”游戏，毽子从一人传给另一人就记为一次踢毽．
若从甲开始，经过三次踢毽后，毽子踢到乙处的概率是多少？请说明理由；
若经过三次踢毽后，毽子踢到乙处的可能性最小，则应从______开始踢．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
