
分析 先把括号里面的式子进行通分,再把除法转化成乘法,然后进行约分,最后找一个适当的值代入计算即可.
解答 解:(x+1-$\frac{15}{x-1}$)÷$\frac{{x}^{2}-8x+16}{1-x}$
=[$\frac{(x+1)(x-1)}{x-1}$-$\frac{15}{x-1}$]÷$\frac{{x}^{2}-8x+16}{1-x}$
=$\frac{(x+1)(x-1)-15}{x-1}$÷$\frac{(x-4)^{2}}{1-x}$
=$\frac{{x}^{2}-16}{x-1}$×$\frac{1-x}{(x-4)^{2}}$
=$\frac{(x+4)(x-4)}{x-1}$×$\frac{1-x}{(x-4)^{2}}$
=$\frac{x+4}{4-x}$,
当x=2时,原式=$\frac{2+4}{4-2}$=3.
点评 此题考查了分式的化简求值,用到的知识点是通分、约分、因式分解、平方差公式、完全平方公式;解答此题的关键是把分式化到最简,然后找一个合适的值代入.


 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,长方形ABCD中,AB=x2+4x+3,设长方形面积为S.
如图,长方形ABCD中,AB=x2+4x+3,设长方形面积为S.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
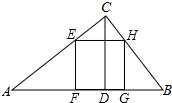 如图,在△ABC中,已知CD为边AB上的高,正方形EFGH的四个顶点分别在△ABC上,求证:$\frac{1}{AB}=\frac{1}{CD}=\frac{1}{EF}$.
如图,在△ABC中,已知CD为边AB上的高,正方形EFGH的四个顶点分别在△ABC上,求证:$\frac{1}{AB}=\frac{1}{CD}=\frac{1}{EF}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com