
【题目】如图,正方形![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,且
上,且![]() ,将
,将![]() 沿
沿![]() 对折至
对折至![]() ,延长
,延长![]() 交边
交边![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,则下列结论:①
,则下列结论:①![]() ≌
≌![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中正确的个数是( )个
,其中正确的个数是( )个
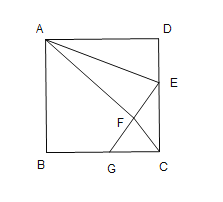
A.1B.2C.3D.4
【答案】C
【解析】
根据翻折变换的性质和正方形的性质可证Rt△ABG≌Rt△AFG;在直角△ECG中,根据勾股定理可证BG=GC;通过证明∠AGB=∠AGF=∠GFC=∠GCF,由平行线的判定可得AG∥CF;求得∠GAF=45°,即可得到∠AGB+∠AED=180°-∠GAF=135°.
∵△AFE是由△ADE折叠得到,
∴AF=AD,∠AFE=∠AFG=∠D=90°,
又∵四边形ABCD是正方形,
∴AB=AD,∠B=∠D,
∴AB=AF,∠B=∠AFG=90°,
在Rt△ABG和Rt△AFG中,
∵![]() ,
,
∴Rt△ABG≌Rt△AFG(HL),
故①正确;
∵正方形ABCD中,AB=6,CD=3DE,
∵EF=DE=![]() CD=2,
CD=2,
设BG=FG=x,则CG=6-x.
在直角△ECG中,根据勾股定理,得(6-x)2+42=(x+2)2,
解得x=3.
∴BG=3,CG=6-3=3;
∴BG=CG;
∴②正确.
∵CG=BG,BG=GF,
∴CG=GF,
∴△FGC是等腰三角形,∠GFC=∠GCF.
又∵Rt△ABG≌Rt△AFG;
∴∠AGB=∠AGF,∠AGB+∠AGF=2∠AGB=180°-∠FGC=∠GFC+∠GCF=2∠GFC=2∠GCF,
∴∠AGB=∠AGF=∠GFC=∠GCF,
∴AG∥CF;
∴③正确
∵∠BAG=∠FAG,∠DAE=∠FAE,
又∵∠BAD=90°,
∴∠GAE=45°,
∴∠AGB+∠AED=180°-∠GAE=135°.
∴④错误.
故选:C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】若将一幅三角板按如图所示的方式放置,则下列结论中不正确的是( )

A. ∠1=∠3 B. 如果∠2=30°,则有AC∥DE
C. 如果∠2=30°,则有BC∥AD D. 如果∠2=30°,必有∠4=∠C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.AO交⊙O于点E,延长AO交⊙O于点D,tanD= ![]() ,
,
(1)求 ![]() 的值.
的值.
(2)设⊙O的半径为3,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为 ![]() ,点A,B,E在x轴上,若正方形BEFG的边长为6,则点C的坐标为( )
,点A,B,E在x轴上,若正方形BEFG的边长为6,则点C的坐标为( )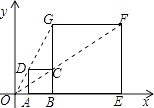
A.(2,2)
B.(3,1)
C.(3,2)
D.(4,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=2![]() ,O是BC边的中点,点E是正方形内一动点,OE=2,连接DE,将线段DE绕点D逆时针旋转90°得DF,连接AE,CF
,O是BC边的中点,点E是正方形内一动点,OE=2,连接DE,将线段DE绕点D逆时针旋转90°得DF,连接AE,CF

(1)如图1,求证:AE=CF;
(2)如图2,若A,E,O三点共线,求点F到直线BC的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强学生的爱国意识,某中学举办“爱我中华”朗诵比赛,全校学生都参加,并对表现优异的学生进行表彰,设置一、二、三等奖和进步奖共四个奖项,赛后,校统计小组随机抽取了九年级两个班级,并将这两个班的获奖情况绘制成以下两幅不完整的统计图.
请根据图中的信息,解答下列问题:
(1)求本次调查抽取的学生人数,并补全条形统计图;
(2)在扇形统计图中,表示“三等奖”的扇形所对应的圆心角度数是 72 °.
(3)若该校共有2600名学生,试估计得奖的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一枚质地均匀的正四面体骰子,它的四个面上分别标有数字0,1,2,3,如图2,正方形ABCD的四个顶点处均有一个圈.课间,李丽和王萍利用它们玩跳圈游戏,玩法如下:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形ABCD的边顺时针分钟连续跳几个边长.
例如:若从圈A起跳,第一掷得的数字为2,便沿正方形的边顺时针连续跳2个边长,落到圈C,第二次掷得的数字为3,便从圈C开始,沿正方形的边顺时针连续跳3个边长,落到圈B,….
设她们从圈A起跳.
(1)若李丽随机掷这枚骰子一次,求她跳回圈A的概率;
(2)若王萍随机掷这枚骰子两次,请用列表法或画树状图求她最后跳回圈A的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某造纸企业为了更好地处理污水问题,决定购买10台新型污水处理设备.甲、乙两种型号的设备可选,其中每台的价格,月处理污水量如表:
A型 | B型 | |
价格(万元/) | 10 | 8 |
处理污水量(吨/月) | 180 | 150 |
(1)经预算:该企业购买污水处理设备的资金不超过85万元,你认为该企业有哪几种购买方案.
(2)在(1)的条件下,若每月需要处理的污水不低于1530吨,为了节约资金,请你为该企业设计一种最省钱的购买方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com