【题目】如图是甲、乙两车在某时段速度随时间变化的图象，下列结论错误的是（ ）
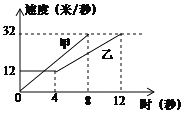
A. 乙前4秒行驶的路程为48米 B. 两车到第3秒时行驶的路程相等
C. 在0到8秒内甲的速度每秒增加4米/秒 D. 在4至8秒内甲的速度都大于乙的速度
【答案】B
【解析】分析：前4s内，乙的速度-时间图象是一条平行于x轴的直线，即速度不变，速度×时间=路程．求出两图象的交点坐标，3秒时两速度大小相等，3s前甲的图象在乙的下方，所以3秒前路程不相等；甲是一条过原点的直线，则速度均匀增加；图象在上方的，说明速度大．
详解：A、根据图象可得，乙前4秒的速度不变，为12米/秒，则行驶的路程为12×4=48米，故A正确；
B、由于甲的图象是过原点的直线，斜率为4，所以可得v=4t（v、t分别表示速度、时间），将v=12m/s代入v=4t得t=3s，则t=3s前，甲的速度小于乙的速度，所以两车到第3秒时行驶的路程不相等，故B错误；
C、根据图象得：在0到8秒内甲的速度是一条过原点的直线，即甲的速度从0均匀增加到32米/秒，则每秒增加
=4米/秒，故C正确；
D、在4至8秒内甲的速度图象一直在乙的上方，所以甲的速度都大于乙的速度，故D正确；
由于该题选择错误的，
故选B．
口算心算速算应用题系列答案
同步拓展阅读系列答案科目：初中数学 来源： 题型：
【题目】如图，正方形OABC的兩辺OA、0C分別在x轴、y轴上，点D(5，3)在边AB上，以Cカ中心，把△CDB旋转90°，则旋转后点D的对应点D′的坐标是（ ）
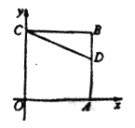
A. (1，10)B. (-2，0)C. (2，10)或(-2，0)D. (10，2)或(-2，0)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知BC∥DE，BF平分∠ABC，DC平分∠ADE，则下列结论：①∠ACB＝∠E；②DF平分∠ADC；③∠BFD＝∠BDF；④∠ABF＝∠BCD，其中正确的有( )
A. 4个B. 3个C. 2个D. 1个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】甲、乙两个批发店销售同一种苹果，甲批发店的价格为每千克6元.在乙批发店，一次购买数量不超过
时，价格为每千克7元；一次购买数量超过时，其中有的价格为每千克7元，超过部分的价格为每千克5元，设小王在同个批发店一次购买苹果的数量为
.
（1）填表：
一次购买苹果的数量（单位： | 20 | 50 | 100 | … |
甲批发店花费（单位：元） | 300 | … | ||
乙批发店花费（单位：元） | 350 | … |
（2）分别用含
的代数式表示甲、乙批发店所花费的钱数.
（3）如果小王在同一个批发店一次购买苹果的数量为
，通过计算说明他在甲、乙两个批批发店所花费的钱数少？
查看答案和解析>>
科目：初中数学 来源： 题型：
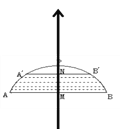
【题目】如右图所示，有一座拱桥圆弧形，它的跨度AB为60米，拱高PM为18米，当洪水泛滥到跨度只有30米时，就要采取紧急措施，若拱顶离水面只有4米，即PN=4米时，是否采取紧急措施？（
）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】随着“中国诗词大会”节目的热播，《唐诗宋词精选》一书也随之热销．如果一次性购买10本以上，超过10本的那部分书的价格将打折，并依此得到付款金额y（单位：元）与一次性购买该书的数量x（单位：本）之间的函数关系如图所示，则下列结论错误的是（ ）
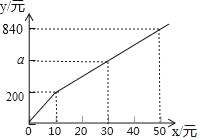
A. 一次性购买数量不超过10本时，销售价格为20元/本
B. a＝520
C. 一次性购买10本以上时，超过10本的那部分书的价格打八折
D. 一次性购买20本比分两次购买且每次购买10本少花80元
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）阅读理解：
如图①，在△ABC中，若AB=10，AC=6，求BC边上的中线AD的取值范围．
解决此问题可以用如下方法：延长AD到点E使DE=AD，再连接BE（或将△ACD绕着点D逆时针旋转180°得到△EBD），把AB、AC，2AD集中在△ABE中，利用三角形三边的关系即可判断．
中线AD的取值范围是 ；
（2）问题解决：
如图②，在△ABC中，D是BC边上的中点，DE⊥DF于点D，DE交AB于点E，DF交AC于点F，连接EF，求证：BE+CF＞EF；
（3）问题拓展：
如图③，在四边形ABCD中，∠B+∠D=180°，CB=CD，∠BCD=140°，以为顶点作一个70°角，角的两边分别交AB，AD于E、F两点，连接EF，探索线段BE，DF，EF之间的数量关系，并加以证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下面材料：如图，点A、B在数轴上分别表示有理数a、b，则A、B两点之间的距离可以表示为|a﹣b|.
根据阅读材料与你的理解回答下列问题：
(1)数轴上表示3与﹣2的两点之间的距离是 .
(2)数轴上有理数x与有理数7所对应两点之间的距离用绝对值符号可以表示为 .
(3)代数式|x+8|可以表示数轴上有理数x与有理数 所对应的两点之间的距离；若|x+8|=5，则x= .
(4)求代数式|x+1008|+|x+504|+|x﹣1007|的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
