
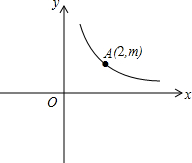
 在平面直角坐标系xOy中,反比例函数y=$\frac{k}{x}$(k>0)的图象经过点A(2,m),连接OA,在x轴上有一点B,且AO=AB,△AOB的面积为2.
在平面直角坐标系xOy中,反比例函数y=$\frac{k}{x}$(k>0)的图象经过点A(2,m),连接OA,在x轴上有一点B,且AO=AB,△AOB的面积为2.分析 (1)把(2,m)代入反比例函数,可得k=2m,且m>0,再根据△AOB的面积为2可得$\frac{1}{2}×4•m=2$,解可得m,进而可求k;
(2)据图可得点C有两个,坐标分别是(0,1+$2\sqrt{3}$)或C(0,1-$2\sqrt{3}$).
解答 解:(1)由题意可知B(4,0),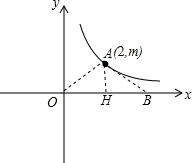 过A作AH⊥x轴于H.
过A作AH⊥x轴于H.
∵${S_{△AOB}}=\frac{1}{2}OB•AH=2$,AH=m,OB=4,
∴$\frac{1}{2}×4•m=2$,
∴m=1,
∴A(2,1),
∴k=2.
(2)C(0,1+$2\sqrt{3}$)或C(0,1-$2\sqrt{3}$).
点评 本题考查了反比例函数的知识,解题的关键是理解点和函数的关系,并能依题意画图,要考虑两种情况.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
 已知图中的曲线是反比例函数y=$\frac{m}{x}$图象上的一支,如果A(a1,b1),B(a2,b2)两点在该反比例函数图象的同一支上,且a1>a2,那么b1<b2.
已知图中的曲线是反比例函数y=$\frac{m}{x}$图象上的一支,如果A(a1,b1),B(a2,b2)两点在该反比例函数图象的同一支上,且a1>a2,那么b1<b2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
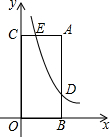 已知,如图,点A($\sqrt{3}$,3),AB⊥x轴于点B,AC⊥y轴于点C,反比例函数y=$\frac{k}{x}$(x>0)的图象与线段AB、AC分别交于D、E.若AB=3BD,则点E的横坐标为$\frac{\sqrt{3}}{3}$.
已知,如图,点A($\sqrt{3}$,3),AB⊥x轴于点B,AC⊥y轴于点C,反比例函数y=$\frac{k}{x}$(x>0)的图象与线段AB、AC分别交于D、E.若AB=3BD,则点E的横坐标为$\frac{\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
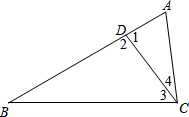 如图,△ABC中,D为AB上一点.已知△ADC与△DBC的面积比为1:3,且AD=3,AC=6,请求出BD的长度,并完整说明为何∠ACD=∠B的理由.
如图,△ABC中,D为AB上一点.已知△ADC与△DBC的面积比为1:3,且AD=3,AC=6,请求出BD的长度,并完整说明为何∠ACD=∠B的理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | “任意画出一个圆,它是中心对称图形”是随机事件 | |
| B. | 为了解我省中学生的体能情况,应采用普查的方式 | |
| C. | 天气预报明天下雨的概率是99%,说明明天一定会下雨 | |
| D. | 任意掷一枚质地均匀的硬币10次,正面朝上的次数不一定是5次 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在?ABCD中,对角线AC、BD相交于点O,点E、F分别是AD、CD的中点,则△OEF的面积S1与△BOC面积S2的关系是( )
如图,在?ABCD中,对角线AC、BD相交于点O,点E、F分别是AD、CD的中点,则△OEF的面积S1与△BOC面积S2的关系是( )| A. | S1=S2 | B. | S1>S2 | C. | S1<S2 | D. | $S1=\frac{1}{2}S2$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
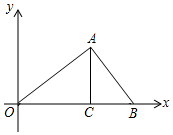 在如图所示的直角坐标系xOy中,AC⊥OB,OA⊥AB,OB=3,点C是OB上靠近O点的三等分点,若反比例函数y=$\frac{k}{x}$(x>0)的图象(图中未画出)与△OAB有两个交点,则k的取值范围是0<k<$\frac{9}{8}\sqrt{2}$.
在如图所示的直角坐标系xOy中,AC⊥OB,OA⊥AB,OB=3,点C是OB上靠近O点的三等分点,若反比例函数y=$\frac{k}{x}$(x>0)的图象(图中未画出)与△OAB有两个交点,则k的取值范围是0<k<$\frac{9}{8}\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com