
【题目】已知抛物线y=ax2+bx+3与x轴分别交于点A(﹣3,0),B(1,0)交于点C,抛物线的顶点为点D.
(1)抛物线的表达式及顶点D的坐标.
(2)若点F是线段AD上一个动点,
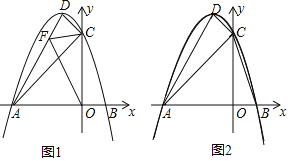
①如图1,当FC+FO的值最小时,求点F的坐标;
②如图2,以点A,F,O为顶点的三角形能否与△ABC相似?若能,求出点F的坐标;若不能,请说明理由.
【答案】(1)y=﹣x2﹣2x+3,(﹣1,4);(2)①F(﹣![]() ,3),②能,(﹣
,3),②能,(﹣![]() ,
,![]() )或(﹣2,2)
)或(﹣2,2)
【解析】
(1)抛物线的表达式为:y=a(x+3)(x﹣1)=a(x2+2x﹣3),故﹣3a=3,解得:a=﹣1,即可求解;再将抛物线解析式化为顶点式即可得出点D的坐标;
(2)①点D的坐标为:(﹣1,4),点A(﹣3,0),点C(0,3),作点O关于直线AD的对称轴R,连接CR交AD于点F,则点F为所求点,即可求解;
②当∠AOF=∠ABC时,△AOF∽△CBA,OF∥BC,直线BC的解析式为y=﹣3x+3,直线OF的解析式为y=﹣3x,直线AD的解析式为y=2x+6,联立直线OF、AD的表达式并解得:x=﹣![]() ,故点F(﹣
,故点F(﹣![]() ,
,![]() );当∠AOF=∠CAB=45°时,△AOF∽△CAB,∠CAB=45°,OF⊥AC,直线OF的解析式为y=﹣x,将上式与y=2x+6联立并解得:x=﹣2,即可求解.
);当∠AOF=∠CAB=45°时,△AOF∽△CAB,∠CAB=45°,OF⊥AC,直线OF的解析式为y=﹣x,将上式与y=2x+6联立并解得:x=﹣2,即可求解.
解:(1)抛物线的表达式为:y=a(x+3)(x﹣1)=a(x2+2x﹣3),
故﹣3a=3,
解得:a=﹣1,
故抛物线的表达式为:y=﹣x2﹣2x+3;
![]()
![]()
![]() 点D的坐标为(﹣1,4)
点D的坐标为(﹣1,4)
(2)①点D的坐标为:(﹣1,4),点A(﹣3,0),点C(0,3),
作点O关于直线AD的对称轴R,连接CR交AD于点F,则点F为所求点,
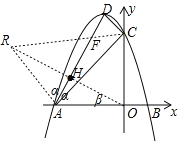
FC+FO=FC+RF=CR为最小,
连接AR,设直线OR交AD于点H,
由点A、D的坐标得,直线AD的表达式为:y=2x+6,
则tan∠DAO=2=tanα,
设∠HOA=∠β,则tanβ=![]() ,则cosβ=
,则cosβ=![]() ,sinβ=
,sinβ=![]() ,
,
OH=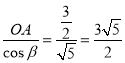 ,OR=2OH=3
,OR=2OH=3![]() ,
,
yR=ORsinβ=3![]() ×
×![]() =3=yC,
=3=yC,
故RC∥x轴,
故yF=3=2x+6,x=﹣![]() ,
,
则点F(﹣![]() ,3);
,3);
②在Rt△ACD中,tan∠CAD![]() ,
,
在Rt△OBC中,tan∠OCB=![]() ,
,
∴∠ACD=∠OCB,
∵OA=OC,
∴∠OAC=∠OCA=45°,
∴∠FAO=∠ACB,
若以A,F,O为顶点的三角形与△ABC相似,则可分两种情况考虑:
当∠AOF=∠ABC时,△AOF∽△CBA,
∴OF∥BC,
设直线BC的解析式为y=kx+b,
将点B、C的坐标代入上式并解得:
直线BC的解析式为y=﹣3x+3,
∴直线OF的解析式为y=﹣3x,
直线AD的解析式为y=2x+6,
联立直线OF、AD的表达式,
解得:x=﹣![]() ,故点F(﹣
,故点F(﹣![]() ,
,![]() ):;
):;
当∠AOF=∠CAB=45°时,△AOF∽△CAB,
∵∠CAB=45°,
∴OF⊥AC,
∴直线OF的解析式为y=﹣x,
将上式与y=2x+6联立并解得:x=﹣2,
故点F(﹣2,2);
综合以上可得F点的坐标为(﹣![]() ,
,![]() )或(﹣2,2).
)或(﹣2,2).


科目:初中数学 来源: 题型:
【题目】我市某蔬菜种植农户购买白菜苗和西红柿苗共1000株,其中白菜苗每株3元,西红柿苗每株5元.已知该农户打算用不少于3600元但不多于3800元的资金购买两种蔬菜.
(1)求该农户可以购买白菜苗株数的最大值和最小值;
(2)该农户按(1)中购买白菜苗株数的最小值的方案购买两种蔬菜苗,经过农户的精心培育,两种蔬菜苗全成活.根据以往的数据分析,平均一株白菜苗可长成2千克白菜,平均一株西红柿苗可结3千克西红柿.农户计划采用直接销售和生态采摘销售两种方式进行销售,其中直接销售白菜的售价为每千克4元,直接销售西红柿的售价为每千克5元;生态采摘销售时两种蔬菜的售价一样,都比直接销售白菜的售价高![]() ,但生态采摘过程中会有
,但生态采摘过程中会有![]() 的损耗.当白菜和西红柿各直接销售一半后、剩下的全部采用生态采摘销售时,该农户可获得8080元的利润.求
的损耗.当白菜和西红柿各直接销售一半后、剩下的全部采用生态采摘销售时,该农户可获得8080元的利润.求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B,图2是点F运动时,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为( )

A. ![]() B. 2 C.
B. 2 C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4张相同的卡片上分别写有数字-1、-3、4、6,将卡片的背面朝上,并洗匀.
(1)从中任意抽取1张,抽到的数字是奇数的概率是 ;
(2)从中任意抽取1张,并将所取卡片上的数字记作一次函数![]() 中的
中的![]() ;再从余下的卡片中任意抽取1张,并将所取卡片上的数字记作一次函数
;再从余下的卡片中任意抽取1张,并将所取卡片上的数字记作一次函数![]() 中的
中的![]() .利用画树状图或列表的方法,求这个一次函数的图象经过第一、二、四象限的概率.
.利用画树状图或列表的方法,求这个一次函数的图象经过第一、二、四象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
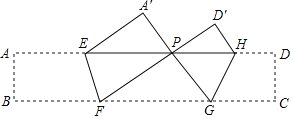
【题目】如图,把矩形ABCD沿EF,GH折叠,使点B,C落在AD上同一点P处,∠FPG=90°,△A′EP的面积是8![]() ,△D′PH的面积是4
,△D′PH的面积是4![]() ,则矩形ABCD的面积等于_____.
,则矩形ABCD的面积等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
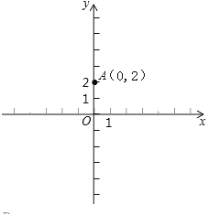
【题目】 如图,在平面直角坐标系中,点![]() ,在x轴上任取一点M,完成以下作图步骤;
,在x轴上任取一点M,完成以下作图步骤;
①连接AM.作线段AM的垂直平分线a.过点M作x轴的垂线b,记![]() 的交点为P:(在答题卡画示意图)
的交点为P:(在答题卡画示意图)
②在x轴上多次改变点M的位置(至少三次),用①的方法得到相应的点P,把这些点用平滑的曲线顺次连接起来,得到曲线C.
(1)猜想曲线C是我们学过的那种曲线,请直接写出你的猜想,
(2)求曲线C的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知抛物线G:y=ax2﹣2ax+4(a≠0).
(1)当a=1时,
①抛物线G的对称轴为x= ;
②若在抛物线G上有两点(2,y1),(m,y2),且y2>y1,则m的取值范围是 ;
(2)抛物线G的对称轴与x轴交于点M,点M与点A关于y轴对称,将点M向右平移3个单位得到点B,若抛物线G与线段AB恰有一个公共点,结合图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
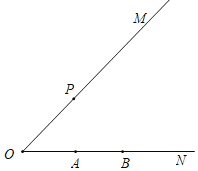
【题目】∠MON=45°,点P在射线OM上,点A,B在射线ON上(点B与点O在点A的两侧),且AB=1,以点P为旋转中心,将线段AB逆时针旋转90°,得到线段CD(点C与点A对应,点D与点B对应).
(1)如图,若OA=1,OP![]() ,依题意补全图形;
,依题意补全图形;
(2)若OP![]() ,当线段AB在射线ON上运动时,线段CD与射线OM有公共点,求OA的取值范围;
,当线段AB在射线ON上运动时,线段CD与射线OM有公共点,求OA的取值范围;
(3)一条线段上所有的点都在一个圆的圆内或圆上,称这个圆为这条线段的覆盖圆.若OA=1,当点P在射线OM上运动时,以射线OM上一点Q为圆心作线段CD的覆盖圆,直接写出当线段CD的覆盖圆的直径取得最小值时OP和OQ的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(t,1)为函数y=ax2+bx+4(a,b为常数,且a≠0)与y=x图象的交点.
(1)求t;
(2)若函数y=ax2+bx+4的图象与x轴只有一个交点,求a,b;
(3)若1≤a≤2,设当![]() ≤x≤2时,函数y=ax2+bx+4的最大值为m,最小值为n,求m﹣n的最小值.
≤x≤2时,函数y=ax2+bx+4的最大值为m,最小值为n,求m﹣n的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com