
| 1 |
| 2 |
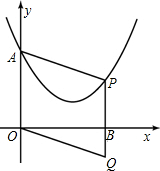 A≤Μ÷ΊΚœΘ°Ν§Ϋ”APΘ§“‘AOΓΔAPΈΣΝΎ±ΏΉςΤΫ––ΥΡ±Ώ–ΈOAPQΘ§PQΥυ‘Ύ÷±œΏ”κx÷αΫΜ”ΎΒψBΘ°…ηΒψPΒΡΚαΉχ±ξΈΣmΘ°
A≤Μ÷ΊΚœΘ°Ν§Ϋ”APΘ§“‘AOΓΔAPΈΣΝΎ±ΏΉςΤΫ––ΥΡ±Ώ–ΈOAPQΘ§PQΥυ‘Ύ÷±œΏ”κx÷αΫΜ”ΎΒψBΘ°…ηΒψPΒΡΚαΉχ±ξΈΣmΘ°| b |
| 2a |
| 4ac-b2 |
| 4a |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


 Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ
Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
 »γΆΦΘ§ΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§OΈΣ÷±Ϋ«»ΐΫ«–ΈABCΒΡ÷±Ϋ«ΕΞΒψΘ§ΓœB=30ΓψΘ§»ώΫ«ΕΞΒψA‘ΎΥΪ«ζœΏy=
»γΆΦΘ§ΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§OΈΣ÷±Ϋ«»ΐΫ«–ΈABCΒΡ÷±Ϋ«ΕΞΒψΘ§ΓœB=30ΓψΘ§»ώΫ«ΕΞΒψA‘ΎΥΪ«ζœΏy=| 1 | x |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
 =2
=2| 3 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
 »γΆΦΘ§ΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§OB‘Ύx÷α…œΘ§ΓœABO=90ΓψΘ§ΒψAΒΡΉχ±ξΈΣΘ®1Θ§2Θ©Θ°ΫΪΓςAOB»ΤΒψAΡφ ±’κ–ΐΉΣ90ΓψΘ§‘ρΒψOΒΡΕ‘”ΠΒψCΒΡΉχ±ξΈΣΘ®ΓΓΓΓΘ©
»γΆΦΘ§ΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§OB‘Ύx÷α…œΘ§ΓœABO=90ΓψΘ§ΒψAΒΡΉχ±ξΈΣΘ®1Θ§2Θ©Θ°ΫΪΓςAOB»ΤΒψAΡφ ±’κ–ΐΉΣ90ΓψΘ§‘ρΒψOΒΡΕ‘”ΠΒψCΒΡΉχ±ξΈΣΘ®ΓΓΓΓΘ©≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
| a+2 |
| SΓςCAD |
| SΓςDGH |
| AD |
| GH |
| FC+2AE |
| 3AM |

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
 »γΆΦ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§AΒψΉχ±ξΈΣΘ®8Θ§0Θ©Θ§BΒψΉχ±ξΈΣΘ®0Θ§6Θ©C «œΏΕΈABΒΡ÷–ΒψΘ°«κΈ ‘Ύy÷α…œ «Ζώ¥φ‘Ύ“ΜΒψPΘ§ ΙΒΟ“‘PΓΔBΓΔCΈΣΕΞΒψΒΡ»ΐΫ«–Έ”κΓςAOBœύΥΤΘΩ»τ¥φ‘ΎΘ§«σ≥ωPΒψΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§ΥΒΟςάμ”…Θ°
»γΆΦ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§AΒψΉχ±ξΈΣΘ®8Θ§0Θ©Θ§BΒψΉχ±ξΈΣΘ®0Θ§6Θ©C «œΏΕΈABΒΡ÷–ΒψΘ°«κΈ ‘Ύy÷α…œ «Ζώ¥φ‘Ύ“ΜΒψPΘ§ ΙΒΟ“‘PΓΔBΓΔCΈΣΕΞΒψΒΡ»ΐΫ«–Έ”κΓςAOBœύΥΤΘΩ»τ¥φ‘ΎΘ§«σ≥ωPΒψΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§ΥΒΟςάμ”…Θ°≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com