
【题目】如图,在五边形ABCDE中,已知∠BAE=120°,∠B=∠E=90°,AB=BC=2,AE=DE=4,在BC、DE上分别找一点M、N,若要使△AMN的周长最小时,则△AMN的最小周长为______.

科目:初中数学 来源: 题型:
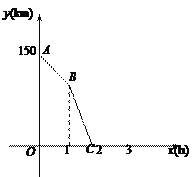
【题目】一辆货车从甲地出发以50 km/h的速度匀速驶往乙地,行驶1 h后,一辆轿车从乙地出发沿同一条路匀速驶往甲地.轿车行驶0.8 h后两车相遇.图中折线ABC表示两车之间的距离y(km)与货车行驶时间x(h)的函数关系.
(1)甲乙两地之间的距离是__________ km,轿车的速度是_________ km/h;
(2)求线段BC所表示的函数表达式;
(3)在图中画出货车与轿车相遇后的y(km)与x(h)的函数图像.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=9,AB=12,BC=15,P为BC边上一动点,PG⊥AC于点G,PH⊥AB于点H.
(1)求证:四边形AGPH是矩形;
(2)在点P的运动过程中,GH的长度是否存在最小值?若存在,请求出最小值,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,将矩形![]() 折叠,使
折叠,使![]() 落在对角线
落在对角线![]() 上,折痕为
上,折痕为![]() ,点
,点![]() 落在点
落在点![]() 处,若
处,若![]() ,则
,则![]() ;
;
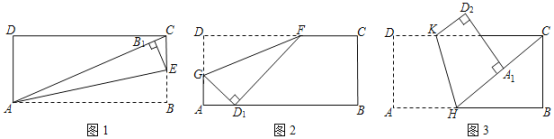
(2)小丽手中有一张矩形纸片,![]() ,
,![]() .她准备按如下两种方式进行折叠:
.她准备按如下两种方式进行折叠:
①如图2,点![]() 在这张矩形纸片的边
在这张矩形纸片的边![]() 上,将纸片折叠,使点
上,将纸片折叠,使点![]() 落在边
落在边![]() 上的点
上的点![]() 处,折痕为
处,折痕为![]() ,若
,若![]() ,求
,求![]() 的长;
的长;
②如图3,点![]() 在这张矩形纸片的边
在这张矩形纸片的边![]() 上,将纸片折叠,使
上,将纸片折叠,使![]() 落在射线
落在射线![]() 上,折痕为
上,折痕为![]() ,点
,点![]() ,
,![]() 分别落在
分别落在![]() ,
,![]() 处,若
处,若![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次消防演习中,消防员架起一架25米长的云梯,如图斜靠在一面墙上,梯子底端离墙7米.

(1)求这个梯子的顶端距地面有多高?
(2)如果消防员接到命令,要求梯子的顶端下降4米(云梯长度不变),那么云梯的底部在水平方向应滑动多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙二人同时从学校出发,沿同一方向匀速行走,![]() 后,甲加快速度继续匀速行走(加速的时间忽略不计),乙始终匀速行走,两人都走了
后,甲加快速度继续匀速行走(加速的时间忽略不计),乙始终匀速行走,两人都走了![]() .两人在行走过程中得到如下表所示的信息:
.两人在行走过程中得到如下表所示的信息:
离开学校的时间 |
|
|
|
|
甲离学校的距离 |
|
|
|
|
乙离学校的距离 |
|
|
|
|
(1)根据题意,甲出发时的速度为_______![]() ,乙的速度为______
,乙的速度为______![]() ;
;
(2)求表中![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
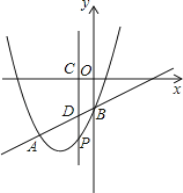
【题目】如图,抛物线y=x2+bx+c与直线y=x﹣1交于A、B两点.点A的横坐标为﹣3,点B在y轴上,点P是y轴左侧抛物线上的一动点,横坐标为m,过点P作PC⊥x轴于C,交直线AB于D.
(1)求抛物线的解析式;
(2)当m为何值时,S四边形OBDC=2S△BPD;
(3)是否存在点P,使△PAD是直角三角形?若存在,求出点P的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次禁毒宣传活动中,某执勤小组乘车沿东西向公路进行安全维护,如果约定向东为正,向西为负,行驶记录如下(单位:米):+18,-9,+7,-14,-3,+13,-8,-6,+15,+6.
(1)执勤过程中,最远处离出发点有多远?
(2)若汽车行驶每千米耗油量为![]() 升,求这次执勤的汽车共耗油多少升?
升,求这次执勤的汽车共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
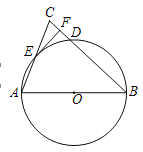
【题目】已知:在△ABC中,AB=BC,以AB为直径作![]() ,交BC于点D,交AC于E,过点E作
,交BC于点D,交AC于E,过点E作![]() 切线EF,交BC于F.
切线EF,交BC于F.
(1)求证:EF⊥BC;
(2)若CD=2,tanC=2,求![]() 的半径.
的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com