
【题目】在![]() 中,
中, ![]() ,点
,点![]() (不与点
(不与点![]() 重合)是线段
重合)是线段![]() 上的一个动点,连接
上的一个动点,连接![]() ,以
,以![]() 为边在
为边在![]() 的右侧作正方形
的右侧作正方形![]() ,连接
,连接![]()
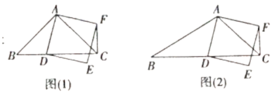
(1)发现问题:如图(1),若![]() ,则
,则![]() 与
与![]() 的位置关系_________;
的位置关系_________;
(2)拓展探究:如图(2),若![]() ,(1)中的结论是否仍然成立?请说明理由;
,(1)中的结论是否仍然成立?请说明理由;
(3)解决问题:若![]() ,设正方形
,设正方形![]() 的边
的边![]() 与线段
与线段![]() 相交于点
相交于点![]() ,请直接写出线段
,请直接写出线段![]() 的最大值
的最大值
【答案】(1)![]() ;(2)仍然成立,见解析;(3)1
;(2)仍然成立,见解析;(3)1
【解析】
(1)由正切值可得∠ACB=45°,结合AB=AC,可知△ABC为等腰直角三角形,再利用正方形的性质可证明△BAD≌△CAF,进而得到∠ACF=45°,推出∠FCB=90°即可得证;
(2)过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,同(1)可证CF⊥BD;
,同(1)可证CF⊥BD;
(3)过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,易证
,易证![]() ,设
,设![]() 为
为![]() ,
,![]() 为
为![]() ,则
,则![]() ,根据对应边成比例建立y与x的函数关系,即可求出CP的最大值.
,根据对应边成比例建立y与x的函数关系,即可求出CP的最大值.
解:(1) ∵![]()
![]()
∵![]() ,
,
![]()
∴![]()
∵四边形![]() 是正方形,
是正方形,
∴![]()
∴![]() ,
,
∴![]() ,
,
在△BAD和△CAF中,
∵AB=AC,∠BAD=∠CAF,AD=AF
∴![]() (SAS),
(SAS),
∴![]() ,
,
∴![]() ,
,
即![]() .
.
(2)(1)中的结论仍然成立,理由如下:
如图(1),过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,则
,则![]() .
.

∵![]() ,
,
∴![]() .
.
∴![]() ,
,
![]()
∴![]()
∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
在△GAD和△CAF中,
∵AG=AC,∠GAD=∠CAF,AD=AF
∴![]() (SAS),
(SAS),
∴![]() ,
,
∴![]() ,即
,即![]() .
.
∴(1)中的结论仍然成立.
(3)线段![]() 的最大值为1.
的最大值为1.
如图(2),过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.

∵![]()
∴![]() .
.
设![]() 为
为![]() ,
,![]() 为
为![]() ,则
,则![]() .
.
由(2)知, ![]() ,
,
∵∠ADE=90°
∴∠ADQ+∠CDP=90°
∵∠DPC+∠CDP=90°
∴∠ADQ=∠DPC
又∵∠AQD=∠DCP=90°,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴当![]() 时,
时, ![]() 有最大值1,
有最大值1,
即线段![]() 的最大值为1.
的最大值为1.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某校九年级数学兴趣小组的学生进行社会实践活动时,想利用所学的解直角三角形的知识测量教学楼的高度,他们先在点D处用测角仪测得楼顶M的仰角为30°,再沿DF方向前行40米到达点E处,在点E处测得楼顶M的仰角为45°,已知测角仪的高AD为1.5米,请根据他们的测量数据求此楼MF的高(结果精确到0.1m,参考数据:![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系x0y中,一次函数y=kx+b(k≠0)的图象与反比例函数![]() (m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n).线段OA=5,E为x轴上一点,且sin∠AOE=
(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n).线段OA=5,E为x轴上一点,且sin∠AOE=![]() .
.
(1)求该反比例函数和一次函数的解析式;
(2)求△AOC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术.其中,方程术是《九章算术》最高的数学成就.《九章算术》“勾股”一章记载:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何?”译文:已知长方形门的高比宽多6尺8寸,门的对角线长1丈,那么门的高和宽各是多少?(1丈=10尺,1尺=10寸)设长方形门的宽![]() 尺,可列方程为_______.
尺,可列方程为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级(1)班要从甲乙两名同学中选派一人去参加学校举行的”扫黑除恶”知识竞赛,王老师准备用一副扑克牌中排列数字分别为![]() ,
,![]() ,
,![]() ,
,![]() 的四张扑克牌做抽数字游戏,决定谁去参加比赛,游戏规则为;将这四张牌的正面全部朝下,洗匀后从中随机抽取一张,得到的数字作为十位上的数字,然后将所抽到的牌放回,再从中随机抽取一张,得到的数字作为个位上的数字,这样就得到了一个两位数,若这个两位数小于
的四张扑克牌做抽数字游戏,决定谁去参加比赛,游戏规则为;将这四张牌的正面全部朝下,洗匀后从中随机抽取一张,得到的数字作为十位上的数字,然后将所抽到的牌放回,再从中随机抽取一张,得到的数字作为个位上的数字,这样就得到了一个两位数,若这个两位数小于![]() ,则甲胜,否则乙获胜,且游戏的获胜者将去参加比赛.
,则甲胜,否则乙获胜,且游戏的获胜者将去参加比赛.
(1)求抽取的扑克牌使得十位数字是![]() 的概率;
的概率;
(2)你认为这个游戏公平吗?请运用概率知识说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
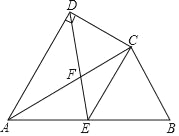
【题目】如图,在四边形ABCD中,AC平分∠DAB,AC2=ABAD,∠ADC=90°,点E为AB的中点.
(1)求证:△ADC∽△ACB.
(2)若AD=2,AB=3,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.了解“乐山市初中生每天课外阅读书籍时间的情况”最适合的调查方式是全面调查
B.甲乙两人跳绳各10次,其成绩的平均数相等,![]() ,则甲的成绩比乙稳定
,则甲的成绩比乙稳定
C.一口袋中装有除颜色外其余均相同的红色小球2个,蓝色小球1个,从中随机一次性摸出2个小球,则恰好摸到同色小球的概率是![]()
D.“任意画一个三角形,其内角和是360°”这一事件是不可能事件
查看答案和解析>>
科目:初中数学 来源: 题型:
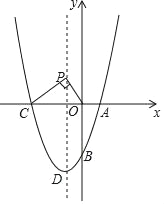
【题目】如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、C两点,点A在点C的右边,与y轴交于点B,点B的坐标为(0,﹣3),且OB=OC,点D为该二次函数图象的顶点.
(1)求这个二次函数的解析式及顶点D的坐标;
(2)如图,若点P为该二次函数的对称轴上的一点,连接PC、PO,使得∠CPO=90°,请求出所有符合题意的点P的坐标;
(3)在对称轴上是否存在一点P,使得∠OPC为钝角,若存在,请直接写出点P的纵坐标为yp的取值范围,若没有,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com