
【题目】已知二次函数![]() ,点
,点![]() 在该函数的图象上,点
在该函数的图象上,点![]() 到
到![]() 轴、
轴、![]() 轴的距离分别为
轴的距离分别为![]() 、
、![]() .设
.设![]() ,下列结论中:
,下列结论中:
①![]() 没有最大值;②
没有最大值;②![]() 没有最小值;③
没有最小值;③![]() 时,
时,![]() 随
随![]() 的增大而增大;
的增大而增大;
④满足![]() 的点
的点![]() 有四个.其中正确结论的个数有( )
有四个.其中正确结论的个数有( )
A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知一抛物线形大门,其地面宽度![]() .一同学站在门内,在离门脚
.一同学站在门内,在离门脚![]() 点
点![]() 远的
远的![]() 处,垂直地面立
处,垂直地面立
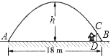
起一根![]() 长的木杆,其顶端恰好顶在抛物线形门上
长的木杆,其顶端恰好顶在抛物线形门上![]() 处.根据这些条件,请你求出该大门的高
处.根据这些条件,请你求出该大门的高![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(m)与挖掘时间x(h)之间的关系如图所示.根据图象所提供的信息有:①甲队挖掘30m时,用了3h;②挖掘6h时甲队比乙队多挖了10m;③乙队的挖掘速度总是小于甲队;④开挖后甲、乙两队所挖河渠长度相等时,x=4.其中一定正确的有( )
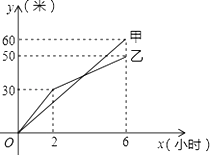
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+2的图象经过点A,且y随x的增大而减小.则A点的坐标可以是( )
A.(2,5)B.(﹣1,1)C.(3,0)D.(![]() ,4)
,4)
查看答案和解析>>
科目:初中数学 来源: 题型:
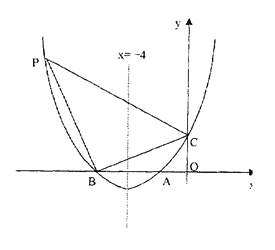
【题目】如图,已知抛物线的对称轴是x=-4,抛物线与x轴交于A,B两点,与y轴交于C点,O是坐标原点,且A,C的坐标分别是(-2,0),(0,3).
(1)求抛物线的解析式;
(2)抛物线上有一点是P,满足∠PBC=90,求P点的坐标;
(3)y轴上是否存在点E使得△AOE与△PBC相似?若存在求出点E的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,BA=BC,CO⊥AB于点O,AO=4,BO=6.
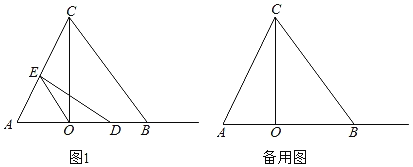
(1)求BC,AC的长;
(2)若点D是射线OB上的一个动点,作DE⊥AC于点E,连结OE.
①当点D在线段OB上时,若△AOE是以AO为腰的等腰三角形,请求出所有符合条件的OD的长.
②设DE交直线BC于点F,连结OF,CD,若S△OBF:S△OCF=1:4,则CD的长为 (直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC是三边都不相等的三角形,点O和点P是这个三角形内部两点.
(1)如图①,如果点P是这个三角形三个内角平分线的交点,那么∠BPC和∠BAC有怎样的数量关系?请说明理由;
(2)如图②,如果点O是这个三角形三边垂直平分线的交点,那么∠BOC和∠BAC有怎样的数量关系?请说明理由;
(3)如图③,如果点P(三角形三个内角平分线的交点),点O(三角形三边垂直平分线的交点)同时在不等边△ABC的内部,那么∠BPC和∠BOC有怎样的数量关系?请直接回答.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场一品牌服装,销售一件可获利![]() 元,为在十一期间增加盈利,进行促销活动,决定采取降价措施.根据以往销售经验及市场调查发现,每件服装降价
元,为在十一期间增加盈利,进行促销活动,决定采取降价措施.根据以往销售经验及市场调查发现,每件服装降价![]() (元)与每天的销售量
(元)与每天的销售量![]() (件)之间的关系如下表
(件)之间的关系如下表
|
|
|
|
|
| … |
|
|
|
|
|
| … |
![]() 请你按照上表,求
请你按照上表,求![]() 与
与![]() 之间的函数解析式.
之间的函数解析式.
![]() 为保证每天能盈利
为保证每天能盈利![]() 元,又能吸引顾客,每件服装应降价多少元?
元,又能吸引顾客,每件服装应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点O是等腰直角三角形ABC斜边上的中点,AB=BC,E是AC上一点,连结EB.
(1) 如图1,若点E在线段AC上,过点A作AM⊥BE,垂足为M,交BO于点F.求证:OE=OF;
(2)如图2,若点E在AC的延长线上,AM⊥BE于点M,交OB的延长线于点F,其它条件不变,则结论“OE=OF”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com