Question

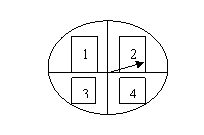
有一个可以自由转动的转盘，被分成了4个相同的扇形，分别标有数1、2、3、4（如图所示）另一个不透明的口袋装有分别标有数0、1、3的三个小球（出数不同外，其余都相同）。小亮转动一次转盘，停止后指针指向木一扇形，扇形内的数是小亮的幸运数，小红任意摸出一个小球，小球上的数是小红的吉祥数，然后计算这两个数的积

（1）请你用画树状图或列表的方法，求这两个数的积为0的概率。

（2）小亮和小红做游戏，规则是：若这两个数的积为奇数，小亮赢；否则，小红赢。你认为该游戏公平吗？为什么？如果不公平，请你修改该游戏规则，使游戏公平。

Answer 1

解：（1）列表如下

	1	2	3	4
0	0	0	0	0
1	1	2	3	4
3	3	6	9	12

由表知，所有可能的结果有12种，其中积为零的有4种，所以极为0的概率为

P==。

（2）不公平。由表中可知极为奇数的有4种，极为偶数的有8种。所以，即为奇数的概率为P₁==.极为偶数的概率为P₂==。因为≠，所以游戏不公平。

游戏规则可修改为：

若这两个数的积为0，则小亮赢；极为奇数，则小红赢。（只要正确即可）