
 已知关于x的函数y=ax2-2abx+ab2-1,直线y=-ax+3与y轴交于点A,与x轴的正半轴交于点P,点B的纵坐标为3,且AP⊥BP,AP=BP.
已知关于x的函数y=ax2-2abx+ab2-1,直线y=-ax+3与y轴交于点A,与x轴的正半轴交于点P,点B的纵坐标为3,且AP⊥BP,AP=BP.分析 (1)根据AP⊥BP,AP=BP先判断出△PAB是等腰直角三角形,确定出点B,P的坐标.
(2)先确定出抛物线的顶点坐标,然后确定出抛物线与直线AB的交点坐标,根据图象确定出b的范围.
解答 解:过P作PC⊥AB,
∵AP⊥BP,AP=BP,
∴△APB为等腰直角三角形,
∴直线y=-ax+3与y轴交于点A,
∴点A的纵坐标为3,
∵点B的纵坐标为3,
∴AB∥x轴,
∴PC=3
∴AB=2PC=6,
∴B(6,3),P(3,0),
∵直线y=-ax+3与x轴的正半轴交于点P,
∴-3a+3=0,
∴a=1,
(2)如图,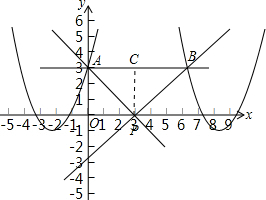
由(1)有a=1,
∴关于x的函数y=ax2-2abx+ab2-1=x2-2bx+b2-1=(x-b)2-1,
∴此函数图象是顶点的纵坐标为-1的抛物线,
∵直线AB解析式为y=3,
∴抛物线与直线AB的交点坐标为(b-2,3)和(b+2,3)
∴两交点之间的距离为4,
∵该二次函数的图象与线段AB只有一个公共点,
∴①当抛物线和线段AB的左侧只交一个点时,
∴b-2<0,b+2≥0,
∴-2≤b<2,
②当抛物线和线段AB的左侧只交一个点时,
∴b-2<≤6,b+2>6,
∴4<b≤8.
∴实数b的取值范围-2≤b<2或4<b≤8.
点评 此题是抛物线的交点坐标题,主要考查了等腰直角三角形的性质,抛物线与直线的交点,解本题的关键是画出图象,分析抛物线与线段AB只有一个交点是解本题的难点.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
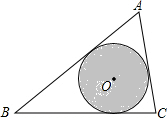 如图,△ABC中,AB=8,AC=5,∠A=60°,圆O是三角形的内切圆,如果在这个三角形内随意抛一粒豆子,则豆子落在圆O内的概率为$\frac{\sqrt{3}π}{10}$.
如图,△ABC中,AB=8,AC=5,∠A=60°,圆O是三角形的内切圆,如果在这个三角形内随意抛一粒豆子,则豆子落在圆O内的概率为$\frac{\sqrt{3}π}{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
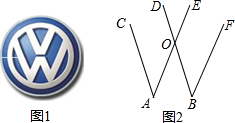 如图,图1是大众汽车的图标,图2反映其中直线间的关系,且AC∥BD,AE∥BF.
如图,图1是大众汽车的图标,图2反映其中直线间的关系,且AC∥BD,AE∥BF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
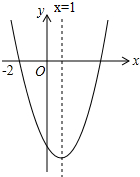 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②2a+b=0;③a+c>b;④抛物线与x轴的另一个交点为(3,0).其中正确的结论有( )个.
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②2a+b=0;③a+c>b;④抛物线与x轴的另一个交点为(3,0).其中正确的结论有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -a<-b | B. | ac<bc | C. | a-1<b-1 | D. | $\frac{a}{3}$>$\frac{b}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com