
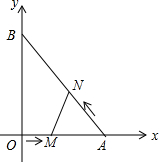
 ��ͼ����ƽ��ֱ������ϵ�У�ֱ��������AOB�Ķ���A��B�ֱ������������ϣ�OΪԭ�㣬��A������Ϊ��6��0������B������Ϊ��0��8��������M�ӵ�O��������OA���յ�A��ÿ��1����λ���ٶ��˶���ͬʱ����N�ӵ�A��������AB���յ�B��ÿ��$\frac{5}{3}$����λ���ٶ��˶�����һ�����㵽���յ�ʱ����һ������Ҳ��ֹ֮ͣ�˶����趯��M��N�˶���ʱ��Ϊt�루t��0����
��ͼ����ƽ��ֱ������ϵ�У�ֱ��������AOB�Ķ���A��B�ֱ������������ϣ�OΪԭ�㣬��A������Ϊ��6��0������B������Ϊ��0��8��������M�ӵ�O��������OA���յ�A��ÿ��1����λ���ٶ��˶���ͬʱ����N�ӵ�A��������AB���յ�B��ÿ��$\frac{5}{3}$����λ���ٶ��˶�����һ�����㵽���յ�ʱ����һ������Ҳ��ֹ֮ͣ�˶����趯��M��N�˶���ʱ��Ϊt�루t��0�������� ��1����NC��OA��C����Rt��ANC�У����NC��AC���ɽ�����⣻
��2������N��NC��OA��C�������⣬AN=$\frac{5}{3}$t��AM=OA-OM=6-t��NC=NA•sin��BAO=$\frac{5}{3}$t•$\frac{4}{5}$=$\frac{4}{3}$t����S��MNA=$\frac{1}{2}$AM•NC=$\frac{1}{2}$����6-t����$\frac{4}{3}$t=-$\frac{2}{3}$��t-3��2+6�����ݶ��κ��������ʼ��ɽ�����⣻
��3�����������η����г����̼��ɽ�����⣮��
���  �⣺��1����NC��OA��C��
�⣺��1����NC��OA��C��
��t=3ʱ��AN=3��$\frac{5}{3}$=5��
��CN=AN•sin��OAB=5��$\frac{4}{5}$=4��AC=AN•cos��OAB=5��$\frac{3}{5}$=3��
��OC=OA-AC=3��
��N��3��4��
�ʴ�ΪN��3��4����
��2������N��NC��OA��C��
�����⣬AN=$\frac{5}{3}$t��AM=OA-OM=6-t��
NC=NA•sin��BAO=$\frac{5}{3}$t•$\frac{4}{5}$=$\frac{4}{3}$t��
��S��MNA=$\frac{1}{2}$AM•NC=$\frac{1}{2}$����6-t����$\frac{4}{3}$t��
=-$\frac{2}{3}$��t-3��2+6��
���MNA����������ֵ�������ֵΪ6��
��3�����ⷨ1��AM=6-t��AN=$\frac{5}{3}$t ��0��t��6����
��AC=AN•cos��BAO=t��
�ٵ�AM=ANʱ��6-t=$\frac{5}{3}$t���� t=$\frac{9}{4}$��
�ڵ�MN=ANʱ����NC��ֱƽ���߶�MA��
��MC=AC=t
��OM+MC+CA=OA
��t+t+t=6 ���t=2
�۵�MN=MAʱ����DΪ�߶�AN���е㣬�� MD��ֱƽ���߶�AN
��AD=$\frac{1}{2}$AN=$\frac{5}{6}t$��
�֡�cos��DAM=cos��OAB ����ߡ�DAM�ס�OAB��
��$\frac{AD}{AM}=\frac{OA}{AB}$�� $\frac{{\frac{5}{6}t}}{6-t}=\frac{6}{10}$��� t=$\frac{108}{43}$��
���ϣ���t��ֵȡ 2��$\frac{9}{4}$��$\frac{108}{43}$ʱ����MAN�ǵ��������Σ�
���ⷨ2��AN=$\frac{5}{3}$t��NC=$\frac{4}{3}$t��AC=AN•cos��BAO=t��
��OC=OA-AC=6-t��
��MC=|OC-OM|=|6-t-t|=|6-2t|
Rt��NCM�� NM2=MC2+NC2
��NM=$\sqrt{{{��6-2t��}^2}+{{��\frac{4}{3}t��}^2}}$=$\sqrt{\frac{52}{9}{t}^{2}-24t+36}$��
��$N{M^2}=\frac{52}{9}{t^2}-24t+36$��
�֣�AM=6-t��AN=$\frac{5}{3}$t��0��t��6����
�ٵ�MN=ANʱ��MN2=AN2
��$\frac{52}{9}{t^2}-24t+36$=${��\frac{5}{3}t��^2}$��
����t2-8t+12=0��t1=2��t2=6����ȥ����
�ڵ�MN=MAʱ��MN2=MA2
��$\frac{52}{9}{t^2}-24t+36$=��6-t��2��
����$\frac{43}{9}$t2-12t=0��t1=0����ȥ����t2=$\frac{108}{43}$��
�۵�AM=ANʱ��6-t=$\frac{5}{3}$t����t=$\frac{9}{4}$��
���ϣ���t��ֵȡ 2��$\frac{9}{4}$��$\frac{108}{43}$ ʱ����MAN�ǵ��������Σ�
���� ���⿼���������ۺ��⡢��ֱ�������Ρ�������Ǻ��������ɶ��������������ε��ж������ʡ����κ��������ʵ�֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ�ṹ�����κ��������ֵ���⣬ѧ���ù������̵�˼��˼�����⣬ѧ��������ۣ������п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ���뾶Ϊ2�İ�Բ��ֽƬ������ͼ��ʽ�۵���ʹ���ۺ��Բ�����е�M��Բ��O�غϣ���ͼ����Ӱ���ֵ�����ǣ�������
��ͼ���뾶Ϊ2�İ�Բ��ֽƬ������ͼ��ʽ�۵���ʹ���ۺ��Բ�����е�M��Բ��O�غϣ���ͼ����Ӱ���ֵ�����ǣ�������| A�� | 18$\sqrt{3}$-6�� | B�� | 4$\sqrt{3}$-$\frac{4}{3}$�� | C�� | 9$\sqrt{3}$-$\frac{9}{2}$�� | D�� | 2$\sqrt{3}$-$\frac{2}{3}$�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ��ֲ���� | 100 | 400 | 750 | 1500 | 3500 | 7000 | 9000 | 14000 |
| �ɻ��� | 83 | 314 | 606 | 1197 | 2810 | 5613 | 7194 | 11208 |
| �ɻ��Ƶ�� | 0.83 | 0.785 | 0.808 | 0.798 | 0.803 | 0.802 | 0.799 | 0.801 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
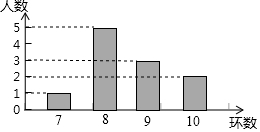 ij������ֲ���11����Ա��ij�����ѵ����ȡ�õijɼ����Ƴ���ͼ��ʾ������ͳ��ͼ����ͼ��֪��11����Ա����ɼ�����λ����8����
ij������ֲ���11����Ա��ij�����ѵ����ȡ�õijɼ����Ƴ���ͼ��ʾ������ͳ��ͼ����ͼ��֪��11����Ա����ɼ�����λ����8�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ���ڰ뾶Ϊ4�ġ�O�У�CD��ֱ����AB���ң���CD��AB������Ϊ��E����AOB=90�㣬����Ӱ���ֵ�����ǣ�������
��ͼ���ڰ뾶Ϊ4�ġ�O�У�CD��ֱ����AB���ң���CD��AB������Ϊ��E����AOB=90�㣬����Ӱ���ֵ�����ǣ�������| A�� | 4��-4 | B�� | 2��-4 | C�� | 4�� | D�� | 2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{3}$ | B�� | $-\frac{1}{3}$ | C�� | 3 | D�� | -3 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com