
分析 (1)设七年一班甲种午餐各订了x盒、乙种午餐各订了y盒,根据:①甲午餐盒数+乙午餐盒数=48,②甲午餐总费用+乙午餐总费用=1000,列方程组求解可得;
(2)设七年二班能买z盒甲种午餐,则乙种午餐有($\frac{1}{3}$z+5)盒,根据:甲午餐总费用+乙午餐总费用≤850,列不等式求解可得.
解答 解:(1)设七年一班甲种午餐各订了x盒、乙种午餐各订了y盒,
根据题意,得:$\left\{\begin{array}{l}{x+y=48}\\{25x+20y=1000}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=8}\\{y=40}\end{array}\right.$,
答:七年一班甲种午餐各订了8盒、乙种午餐各订了40盒.
(2)设七年二班能买z盒甲种午餐,则乙种午餐有($\frac{1}{3}$z+5)盒,
根据题意,得:25z+20($\frac{1}{3}$z+5)≤850
解得:z≤23$\frac{13}{19}$
∵z与$\frac{1}{3}$z+5都是正整数,
∴z的最大值为21.
答:七年二班最多能买21盒甲种午餐.
点评 本题考查了一元一次不等式和二元一次方程组的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程和不等式求解.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| A款手机 | B款手机 | |
| 进货价格(元) | 1100 | 1400 |
| 销售价格(元) | 今年的销售价格 | 2000 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 原料 | 甲 | 乙 |
| 维生素C的含量∕(单位∕kg) | 600 | 100 |
| 原料价格∕(元∕kg) | 8 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
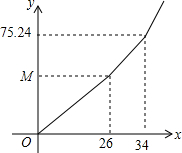 某市为鼓励居民节约用水,实行新的阶梯水价,即按用水量进行分段收费,阶段水价方案主要分为三档:
某市为鼓励居民节约用水,实行新的阶梯水价,即按用水量进行分段收费,阶段水价方案主要分为三档:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com