
【题目】如图,AB∥DE,AC∥DF,AC=DF,添加下列条件,不能判断 △ABC≌△DEF的是( )
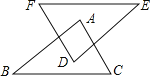
A. EF=BC B. AB=DE C. EF∥BC D. ![]() B=
B=![]() E
E
【答案】A
【解析】
根据全等三角形的判定方法结合所给条件逐项分析即可.
∵AB∥DE,
∴∠1=∠2.
∵AC∥DF,
∴∠1=∠D,
∴∠2=∠D.
A. 在△ABC和△DEF中,
AC=DF,
EF=BC,
∠2=∠D,
此3个条件符合“SSA”,而“SSA”不能作为全等三角形的判定方法,故A不能判断 △ABC≌△DEF;
B. 在△ABC和△DEF中,
AC=DF,
∠2=∠D,
AB=DE,
∴△ABC≌△DEF(SAS),
故B能判断 △ABC≌△DEF;
C.延长BA交FE于点G.
∵EF∥BC,
∴∠3=∠B.
∵AB∥DE,
∴∠3=∠E,
∴∠B=∠E.
在△ABC和△DEF中,
∠B=∠E,
∠2=∠D,
AC=DF,
∴△ABC≌△DEF(AAS),
故C能判断 △ABC≌△DEF;
D. 在△ABC和△DEF中,
∠B=∠E,
∠2=∠D,
AC=DF,
∴△ABC≌△DEF(AAS),
故D能判断 △ABC≌△DEF;
故选A.


科目:初中数学 来源: 题型:
【题目】某星期天下午,小强和小明相约在某公共汽车站一起乘车回学校,小强从家出发先步行到车站,等小明到了后两人一起乘公共汽车回到学校.图中折线表示小强离开家的路程![]() (公里)和所用时间
(公里)和所用时间![]() (分钟)之间的函数关系.下列说法中错误的是( )
(分钟)之间的函数关系.下列说法中错误的是( )
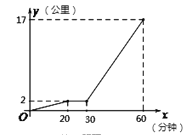
A. 小强从家到公共汽车站步行了2公里 B. 小强在公共汽车站等小明用了10分钟
C. 小强乘公共汽车用了20分钟 D. 公共汽车的平均速度是30公里/小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,矩形![]() 的对角线
的对角线![]() ,
,![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)把矩形![]() 沿直线
沿直线![]() 对折,使点
对折,使点![]() 落在点
落在点![]() 处,折痕
处,折痕![]() 分别与
分别与![]() 、
、![]() 、
、![]() 相交于点
相交于点![]() 、
、![]() 、
、![]() ,求直线
,求直线![]() 的解析式;
的解析式;
(3)若点![]() 在直线
在直线![]() 上,平面内是否存在点
上,平面内是否存在点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?若存在,请直接写出点
为顶点的四边形是菱形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果批发市场有一种高档水果,如果每千克盈利(毛利润)10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销量将减少20千克.
(1)若以每千克能盈利18元的单价出售,问每天的总毛利润为多少元?
(2)现市场要保证每天总毛利润6000元,同时又要使顾客得到实惠,则每千克应涨价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某食品加工厂需要一批食品包装盒,供应这种包装盒有两种方案可供选择:
方案一:从包装盒加工厂直接购买,购买所需的费y1与包装盒数x满足如图1所示的函数关系.
方案二:租赁机器自己加工,所需费用y2(包括租赁机器的费用和生产包装盒的费用)与包装盒数x满足如图2所示的函数关系.根据图象回答下列问题:
(1)方案一中每个包装盒的价格是多少元?
(2)方案二中租赁机器的费用是多少元?生产一个包装盒的费用是多少元?
(3)请分别求出y1、y2与x的函数关系式.
(4)如果你是决策者,你认为应该选择哪种方案更省钱?并说明理由

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ABC=90°,点D,F分别是AC,AB的中点,CE∥DB,BE∥DC.
(1)求证:四边形DBEC是菱形;
(2)若AD=3,DF=1,求四边形DBEC面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
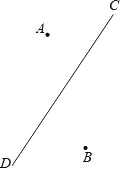
【题目】如图所示,李明和王丽家分别位于公路CD两侧的A,B处,星期天王丽要去为李明送书,他两人约定在公路CD边上见面.李明骑自行车,王丽步行,为节省时间,他们见面的地点定在距离王丽家最近的点E
(1)请你利用所学过的知识,画图确定点E的位置并写出画图依据;
(2)出门前李明发现自行车坏了,临时决定也步行前往,为节省时间,他们约定在距离他两家距离之和最小的F处见面,请你画出图形,确定点F的位置并写出画图依据.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com