
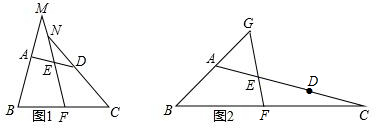
分析 (1)连接BD,取DB的中点H,连接EH,FH,根据三角形中位线定理得到EH∥AB,EH=$\frac{1}{2}$AB,根据平行线的性质证明;
(2)连接BD,取DB的中点H,连接EH,FH,根据勾股定理、平行线的性质计算.
解答 (1)证明:连接BD,取DB的中点H,连接EH,FH,
∵E,H分别是AD,BD的中点,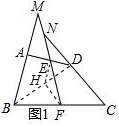
∴EH∥AB,EH=$\frac{1}{2}$AB,
∴∠BME=∠HEF,
∵F,H分别是BC,BD的中点,
∴FH∥CD,FH=$\frac{1}{2}$CD,
∴∠CNE=∠HFE,
∵AB=CD
∴HE=FH,
∴∠HEF=∠HFE
∴∠BME=∠CNE;
(2)连接BD,取DB的中点H,连接EH,FH,
∵E,F分别是AD,BC的中点,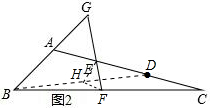
∴EH=$\frac{1}{2}$AB,FH=$\frac{1}{2}$CD,FH∥AC,
∴∠HFE=∠FEC=45°,
∵AB=CD=2,
∴HF=HE=1,
∴∠HEF=∠HFE=45°,
∴∠EHF=180°-∠HFE-HEF=90°,
∴$EF=\sqrt{H{E^2}+H{F^2}}=\sqrt{{1^2}+{1^2}}=\sqrt{2}$.
点评 本题考查的是三角形中位线定理,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
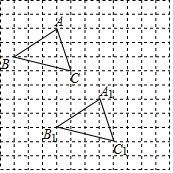 在方格纸中,把一个图形先沿水平方向平移|a|格(当a为正数时,表示向右平移;当a为负数时,表示向左平移),再沿竖直方向平移|b|格(当b为正数时,表示向上平移;当b为负数时,表示向下平移),得到一个新的图形,我们把这个过程记为【a,b】.例如,把图中的ABC先向右平移3格,再向下平移5格得到△A1B1C1,可以把这个过程记为【3,-5】.若再将△A1B1C1经过【4,2】得到△A2B2C2,则△ABC经过平移得到△A2B2C2的过程是( )
在方格纸中,把一个图形先沿水平方向平移|a|格(当a为正数时,表示向右平移;当a为负数时,表示向左平移),再沿竖直方向平移|b|格(当b为正数时,表示向上平移;当b为负数时,表示向下平移),得到一个新的图形,我们把这个过程记为【a,b】.例如,把图中的ABC先向右平移3格,再向下平移5格得到△A1B1C1,可以把这个过程记为【3,-5】.若再将△A1B1C1经过【4,2】得到△A2B2C2,则△ABC经过平移得到△A2B2C2的过程是( )| A. | 【2,7】 | B. | 【7,-3】 | C. | 【7,-7】 | D. | 【-7,-2】 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
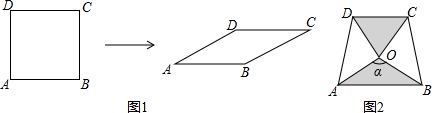
| α | 30° | 45° | 60° | 90° | 120° | 135° | 150° |
| S | $\frac{1}{2}$ | 1 | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
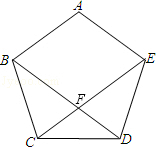 如图,正五边形ABCDE的对角线BD、CE相交于点F,则下列结论正确的是( )
如图,正五边形ABCDE的对角线BD、CE相交于点F,则下列结论正确的是( )| A. | ∠BCE=36° | B. | △BCF是直角三角形 | ||
| C. | △BCD≌△CDE | D. | AB⊥BD |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com