
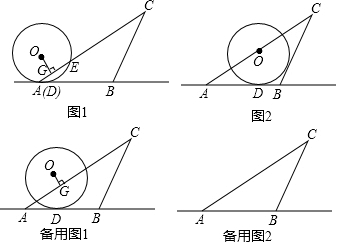
分析 (1)先求出∠OAC=60°,进而得出△OAE是等边三角形即可;
(2)先求出OC=4,再求出∠C=30°,进而求出OH=2=OD即可;
(3)分两种情况,点O在AC左侧和右侧,先利用锐角三角函数表示出FD进而得出OF,最后用锐角三角函数即可得出结论.
解答 解:(1)∵⊙O与直线AB相切于点D,
∴∠ODB=90°,
当点D与点A重合时,
连接OA,OE,
∴OA=OE,
∵∠BAC=30°,
∴∠OAC=60°,
∴△OAE是等边三角形,
∴AE=OA=2,
故答案为2;
(2)BC与⊙O相切,
理由:如图2,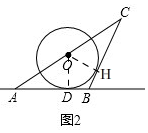 过点O作OH⊥BC于H,连接OD,
过点O作OH⊥BC于H,连接OD,
∵⊙O与AB相切于D,
∴OD⊥AB,
在Rt△AOD中,∠A=30°,
∴OA=2OD=4,
∵AC=8,
∴OC=4,
在△ABC中,AB=AC,
∴∠C=∠BAC=30°,
在Rt△OHC中,∠C=30°,
∴OH=$\frac{1}{2}$OC=2=OD,
∴BC与⊙O相切,
(3)①当点O在AC的左侧时,
连接OD交AC于F,如备用图1,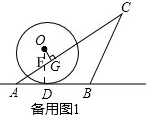
∵⊙O与AB相切于D,
∴OD⊥AB,
∵OG⊥AC,
∴∠FOG=∠BAC=30°,
在Rt△FDA中,tan∠BAC=$\frac{FD}{AD}$,
∴FD=AD•tan∠BAC=$\frac{\sqrt{3}}{3}$x,
∴OF=2-$\frac{\sqrt{3}}{3}$x,
在Rt△FOG中,y=OG=OF•cos∠FOG=(2-$\frac{\sqrt{3}}{3}$x)×$\frac{\sqrt{3}}{2}$=-$\frac{1}{2}$x+$\sqrt{3}$,
x的取值范围为0≤x≤2$\sqrt{3}$;
②当点O在AC的右侧时,
连接DO并延长交AC于F,如备用图2,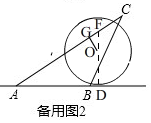 同①的方法得,FD=$\frac{\sqrt{3}}{3}$x,
同①的方法得,FD=$\frac{\sqrt{3}}{3}$x,
∴OF=$\frac{\sqrt{3}}{3}$x-2,
∵FD⊥AB,
∴∠BAC+∠AFD=90°,
∴∠FOG=∠BAC=30°,
在Rt△FOG中,y=OG=OF•cos∠FOG=($\frac{\sqrt{3}}{3}$x-2)×$\frac{\sqrt{3}}{2}$=$\frac{1}{2}$x-$\sqrt{3}$,
x的取值范围为2$\sqrt{3}$≤x≤$\frac{14\sqrt{3}}{3}$.
点评 此题是圆的综合题,主要考查了圆的切线的性质,勾股定理,含30度角的直角三角形的性质,锐角三角函数,等边三角形的判定和性质,解(1)的关键是得出∠OAC=60°,解(2)的关键是求出OH=2,解(3)的关键是分两种情况求出OF,解本题的重点是作出辅助线,是一道中等难度的题目.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
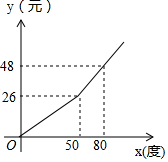 某城市电业局为鼓励居民节约用电,采取按月用电量分段收费办法,居民应交电费y(元)与用电量x(度)的函数关系如图所示.
某城市电业局为鼓励居民节约用电,采取按月用电量分段收费办法,居民应交电费y(元)与用电量x(度)的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
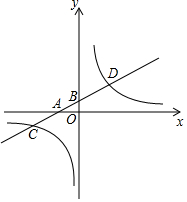 如图,在平面直角坐标系中,一次函数y1=kx+b的图象分别交x轴,y轴于A、B两点,与反比例函数y2=$\frac{n}{x}$的图象交于C、D两点,已知点C的坐标为(-4,-1),点D的横坐标为2.
如图,在平面直角坐标系中,一次函数y1=kx+b的图象分别交x轴,y轴于A、B两点,与反比例函数y2=$\frac{n}{x}$的图象交于C、D两点,已知点C的坐标为(-4,-1),点D的横坐标为2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
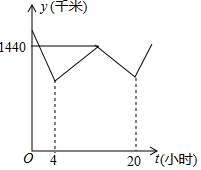 甲、乙两车分别从A、B两地同时出发匀速相向而行,大楼C位于AB之间,甲与乙相遇在AC中点处,然后两车立即掉头,以原速原路返回,直到各自回到出发点.设甲、乙两车距大楼C的距离之和为y(千米),甲车离开A地的时间为t(小时),y与t的函数图象所示,则第21小时时,甲乙两车之间的距离为1350千米.
甲、乙两车分别从A、B两地同时出发匀速相向而行,大楼C位于AB之间,甲与乙相遇在AC中点处,然后两车立即掉头,以原速原路返回,直到各自回到出发点.设甲、乙两车距大楼C的距离之和为y(千米),甲车离开A地的时间为t(小时),y与t的函数图象所示,则第21小时时,甲乙两车之间的距离为1350千米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
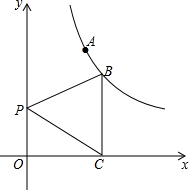 已知点A(1,2)、点 B在双曲线y=$\frac{k}{x}$(x>0)上,过B作BC⊥x轴于点C,如图,P是y轴上一点,
已知点A(1,2)、点 B在双曲线y=$\frac{k}{x}$(x>0)上,过B作BC⊥x轴于点C,如图,P是y轴上一点,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=-2(x-1)2+6 | B. | y=-2(x-1)2-6 | C. | y=-2(x+1)2+6 | D. | y=2(x+1)2-6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
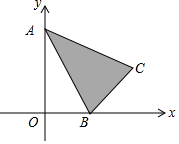 如图,已知△ABC的顶点坐标分别为A(0,2)、B(1,0)、C(2,1),若二次函数y=x2+bx+1的图象与阴影部分(含边界)一定有公共点,则实数b的取值范围是( )
如图,已知△ABC的顶点坐标分别为A(0,2)、B(1,0)、C(2,1),若二次函数y=x2+bx+1的图象与阴影部分(含边界)一定有公共点,则实数b的取值范围是( )| A. | b≤-2 | B. | b<-2 | C. | b≥-2 | D. | b>-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com