
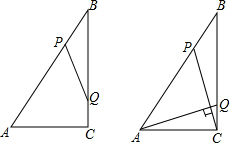
 如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.分析 (1)根据勾股定理即可得到结论;分两种情况:①当△BPQ∽△BAC时,BP:BA=BQ:BC;当△BPQ∽△BCA时,BP:BC=BQ:BA,再根据BP=5t,QC=4t,AB=10cm,BC=8cm,代入计算即可;
(2)分三种情况:①当PB=PQ时,如图1,过P作PH⊥BQ,则BH=$\frac{1}{2}$BQ=4-2t,PB=5t,根据平行线分线段成比例定理得到$\frac{PB}{AB}=\frac{BH}{BC}$,即:$\frac{5t}{10}=\frac{4-2t}{8}$解得t=$\frac{2}{3}$,②当PB=BQ时,即5t=8-4t,解得t=$\frac{8}{9}$,③当BQ=PQ时,如图2,过Q作QG⊥AB于G,则BG=$\frac{1}{2}$PB=$\frac{5}{2}$t,BQ=8-4t,通过△BGQ∽△ACB,得到比例式$\frac{BG}{BC}=\frac{BQ}{AB}$,解得:t=$\frac{64}{57}$.
(3)先利用勾股定理表示出CP2,建立方程求解即可求出时间t;
(4)过P作PM⊥BC于点M,AQ,CP交于点N,则有PB=5t,PM=3t,MC=8-4t,根据△ACQ∽△CMP,得出AC:CM=CQ:MP,代入计算即可.
解答 解:(1)∵∠ACB=90°,AC=6cm,BC=8cm,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=10cm;
分两种情况讨论:
①当△BPQ∽△BAC时,$\frac{BP}{BA}=\frac{BQ}{BC}$,
∵BP=5t,QC=4t,AB=10,BC=8,
∴$\frac{5t}{10}=\frac{8-4t}{8}$,解得,t=1,
②当△BPQ∽△BCA时,$\frac{BP}{BC}=\frac{BQ}{BA}$,
∴$\frac{5t}{8}=\frac{8-4t}{10}$,解得,t=$\frac{32}{41}$;
∴t=1或$\frac{32}{41}$时,△BPQ∽△BCA;
(2)分三种情况:
①当PB=PQ时,如图1,过P作PH⊥BQ,
则BH=$\frac{1}{2}$BQ=4-2t,PB=5t,
∴PH∥AC,
∴$\frac{PB}{AB}=\frac{BH}{BC}$,即$\frac{5t}{10}=\frac{4-2t}{8}$解得:t=$\frac{2}{3}$,
②当PB=BQ时,即5t=8-4t,
解得:t=$\frac{8}{9}$,
③当BQ=PQ时,如图2,过Q作QG⊥AB于G,
则BG=$\frac{1}{2}$PB=$\frac{5}{2}$t,BQ=8-4t,
∵△BGQ∽△ACB,
∴$\frac{BG}{BC}=\frac{BQ}{AB}$即$\frac{\frac{5}{2}t}{8}=\frac{8-4t}{10}$,
解得:t=$\frac{64}{57}$.
综上所述:△BPQ是等腰三角形时t的值为:$\frac{2}{3}$或$\frac{8}{9}$或$\frac{64}{57}$.
(3)过P作PM⊥BC于点M,AQ,CP交于点N,如图3所示:
则PB=5t,PM=3t,MC=8-4t,CQ=4t,
根据勾股定理得,CP2=PM2+MC2=25t2-64t+64,
∵CP=CQ
∴25t2-64t+64=16t2,
∴t=$\frac{64-24\sqrt{2}}{18}$=$\frac{32-12\sqrt{2}}{9}$或t=$\frac{32+12\sqrt{2}}{9}$(舍),
∴CP=CQ时,t=$\frac{32-12\sqrt{2}}{9}$;
(4)过P作PM⊥BC于点M,AQ,CP交于点N,如图3所示
则PB=5t,PM=3t,MC=8-4t,
∵∠NAC+∠NCA=90°,∠PCM+∠NCA=90°,
∴∠NAC=∠PCM,
∵∠ACQ=∠PMC,
∴△ACQ∽△CMP,
∴$\frac{AC}{CM}=\frac{CQ}{MP}$,
∴$\frac{6}{8-4t}=\frac{4t}{3t}$,解得t=$\frac{7}{8}$.
点评 此题是相似形综合题,主要考查了相似三角形的判定与性质,勾股定理,直角三角形的性质,等腰三角形的性质,由三角形相似得出对应边成比例是解题的关键.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:初中数学 来源: 题型:解答题
| 射箭次数 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
| 小明成绩(环) | 6 | 7 | 7 | 7 | 8 |
| 小亮成绩(环) | 4 | 8 | 8 | 6 | 9 |
| 姓名 | 平均数(环) | 众数(环) | 方差 |
| 小明 | 7 | 7 | 0.4 |
| 小亮 | 7 | 8 | 3.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,在正方形ABCD中,E,F分别AB,AD上的点,又AB=12,EF=10,△AEF的面积等于五边形EBCDF面积的$\frac{1}{5}$,求AE,AF的长.
已知:如图,在正方形ABCD中,E,F分别AB,AD上的点,又AB=12,EF=10,△AEF的面积等于五边形EBCDF面积的$\frac{1}{5}$,求AE,AF的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com