
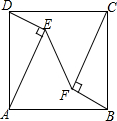
 如图,在正方形ABCD中,分别以AD,BC为斜边作Rt△ADE和Rt△CBF,且Rt△ADE≌Rt△CBF,连结EF,若S正方形ABCD=20,S△ADE=3,则EF=4.
如图,在正方形ABCD中,分别以AD,BC为斜边作Rt△ADE和Rt△CBF,且Rt△ADE≌Rt△CBF,连结EF,若S正方形ABCD=20,S△ADE=3,则EF=4. 分析 作辅助线,构建直角三角形和高线,先根据已知的面积求出正方形边长和ME的长,再根据等量关系式:①DE2+AE2=AD2,②DM+AM=AD,列方程组求出x的值,即DE2=2,再计算EG和FG的长,最后利用勾股定理求EF的长.
解答 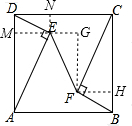 解:如图,过E作EM⊥AD,EN⊥DC,垂足分别为M、N,过F作FH⊥BC于H,过F作BC的平行线与ME的延长线交于点G,
解:如图,过E作EM⊥AD,EN⊥DC,垂足分别为M、N,过F作FH⊥BC于H,过F作BC的平行线与ME的延长线交于点G,
∵四边形ABCD为正方形,
∴AD∥BC,
∴△EGF是直角三角形,
∵S正方形ABCD=20,
∴AD=$\sqrt{20}$=2$\sqrt{5}$,
∵S△ADE=3,
∴$\frac{1}{2}$AD•ME=3,
则$\frac{1}{2}$×2$\sqrt{5}$×ME=3,
∴ME=$\frac{3\sqrt{5}}{5}$,
设DE2=x,AE2=y,
由题意得:$\left\{\begin{array}{l}{x+y=20}\\{\sqrt{x-M{E}^{2}}+\sqrt{y-M{E}^{2}}=\sqrt{20}}\end{array}\right.$,
y=20-x,ME2=($\frac{3\sqrt{5}}{5}$)2=$\frac{9}{5}$,
则$\sqrt{x-\frac{9}{5}}$+$\sqrt{20-x-\frac{9}{5}}$=$\sqrt{20}$,
化简得:x2-20x=-36,
解得:x1=18(舍),x2=2,
∴DE2=2,
∴NE=$\sqrt{D{E}^{2}-D{N}^{2}}$=$\sqrt{2-\frac{9}{5}}$=$\frac{\sqrt{5}}{5}$,
∵Rt△ADE≌Rt△CBF,
∴FH=EM=$\frac{3\sqrt{5}}{5}$,
∴EG=2$\sqrt{5}$-2ME=2$\sqrt{5}$-2×$\frac{3\sqrt{5}}{5}$=$\frac{4\sqrt{5}}{5}$,
FG=2$\sqrt{5}$-2NE=2$\sqrt{5}$-2×$\frac{\sqrt{5}}{5}$=$\frac{8\sqrt{5}}{5}$,
由勾股定理得:EF2=EG2+FG2,
∴EF=$\sqrt{(\frac{4\sqrt{5}}{5})^{2}+(\frac{8\sqrt{5}}{5})^{2}}$=$\sqrt{16}$=4,
故答案为:4.
点评 本题考查了正方形的性质和勾股定理的运用,在四边形中常利用勾股定理求边的长,本题的关键是作辅助线,构建直角三角形和三角形的高线,巧妙地根据勾股定理列方程组,使问题得以解决,另外本题的计算量大,容易出错,要细心.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知矩形ABCD中,AB=4,AD=3,P是以CD为直径的半圆上的一个动点,连接BP,则BP的最大值是$\sqrt{13}$+2.
如图,已知矩形ABCD中,AB=4,AD=3,P是以CD为直径的半圆上的一个动点,连接BP,则BP的最大值是$\sqrt{13}$+2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示的是由5个边长是1的正方形组成的图形.
如图所示的是由5个边长是1的正方形组成的图形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com