
| 1 |
| 4 |
| 1 |
| n |
| 180° |
| n |
| 1 |
| 2 |
| α |
| 4 |
| 3 |
| 4 |
| α |
| n |
| (n-1)α |
| n |
| 1 |
| 2 |
| α |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| (n-1)α |
| n |
| 180° |
| n |
| α |
| n |
| 180° |
| n |
| 180° |
| n |
| α |
| n |
| α |
| n |
| α |
| n |
| (n-1)α |
| n |
| (n-1)α |
| n |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
| A、10 | B、-9 | C、-8 | D、-7 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示为“贾宪三角”的一部分,也称“杨辉三角系数表”,它的作用是指导我们按规律写出形如(a+b)″(其中n为正整数)的展开式中各项的系数,请你仔细观察图中的规律,填写下面(a+b)4,(a+b)5展开式中所缺的系数
如图所示为“贾宪三角”的一部分,也称“杨辉三角系数表”,它的作用是指导我们按规律写出形如(a+b)″(其中n为正整数)的展开式中各项的系数,请你仔细观察图中的规律,填写下面(a+b)4,(a+b)5展开式中所缺的系数查看答案和解析>>
科目:初中数学 来源: 题型:
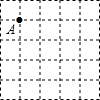 在5×5的正方形方格中,每个小正方形的边长都为1,请在下图给定的网格中按下列要求画出图形.
在5×5的正方形方格中,每个小正方形的边长都为1,请在下图给定的网格中按下列要求画出图形.| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
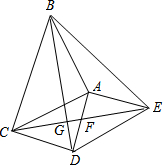 如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连接CE交AD于点F,连接BD交CE于点G,连接BE;下列结论中:①CE=BD;②∠ADB=∠AEB;③△ADC是等腰直角三角形;④CD•AE=EF•CG;一定正确的结论有( )
如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连接CE交AD于点F,连接BD交CE于点G,连接BE;下列结论中:①CE=BD;②∠ADB=∠AEB;③△ADC是等腰直角三角形;④CD•AE=EF•CG;一定正确的结论有( )| A、1个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 有下列四个判断:①AD=BF;②AE=BC;③∠EFA=∠CDB;④AE∥BC.请你以其中三个作为题设,余下一个作为结论,写出一个真命题并加以证明.
有下列四个判断:①AD=BF;②AE=BC;③∠EFA=∠CDB;④AE∥BC.请你以其中三个作为题设,余下一个作为结论,写出一个真命题并加以证明.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠PEF的度数是( )
如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠PEF的度数是( )| A、15° | B、20° |
| C、25° | D、30° |
查看答案和解析>>
科目:初中数学 来源: 题型:
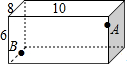 如图所示,在长、宽、高分别为10cm、8cm、6cm的长方体器皿的A点(三等分点)有一只蚂蚁,在B点(四等分点)处有一粒大米,请计算:蚂蚁要吃到大米最少要走多远.
如图所示,在长、宽、高分别为10cm、8cm、6cm的长方体器皿的A点(三等分点)有一只蚂蚁,在B点(四等分点)处有一粒大米,请计算:蚂蚁要吃到大米最少要走多远.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com