
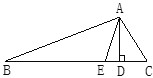
【题目】已知,如图,在△ ABC中,AD,AE分别是 △ ABC的高和角平分线,若∠B=30°,∠C=50°.
(1)求∠DAE的度数.
(2)试写出 ∠DAE与∠C-∠B有何关系?(不必证明)
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在弹性限度内,弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂物体的质量x(kg)之间的关系如下表,下列说法不正确的是( )
x/kg | 0 | 1 | 2 | 3 | 4 | 5 |
y/cm | 20 | 20.5 | 21 | 21.5 | 22 | 22.5 |
A. x与y都是变量,且x是自变量,y是x的函数
B. 弹簧不挂重物时的长度为0 cm
C. 物体质量每增加1 kg,弹簧长度y增加0.5 cm
D. 所挂物体质量为7 kg时,弹簧长度为23.5 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
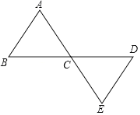
【题目】如图,连接在一起的两个等边三角形的边长都为2cm,一个微型机器人由点A开始按A→B→C→D→E→C→A→B→C…的顺序沿等边三角形的边循环移动.当微型机器人移动了2018cm后,它停在了点_____上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A=100°,BI、CI分别平分∠ABC,∠ACB,则∠BIC=________,若BM、CM分别平分∠ABC,∠ACB的外角平分线,则∠M=__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把两个大小相等,形状相同的两个三角形称之为全等三角形,如果两个三角形仅仅是形状相同,我们可以称之为相似三角形,如图①△ABC与△DEF形状相同,我们就可以说△ABC 与△DEF相似,记作△ABC∽△DEF,点A与点D、点B与点E、点C与点F分别是对应点。下面我们就相似三角形的知识进行一些简单的探索。

(1)观察下列图②两组图形,相似的一组是 。

(2)如图③,小明用一张纸遮住了3个三角形的一部分,你是可以画出这3个三角形的。

提出问题:①如图,如果∠A=∠C,∠B=∠D,AB=CD,那么第一个三角形与第二个三角形全等吗?你的判断是 ,(填“是”或“否”)判断的依据是 。
②如图,如果∠A=∠E,∠B=∠F,2AB=EF,那么第一个三角形与第三个三角形相似吗?你的判断是 ,(填“是”或“否”)
(3)由(1)、(2)你可以得出的结论是:有 个角分别相等的两个三角形相似。
(4)用(3)的结论解决下面两个问题.
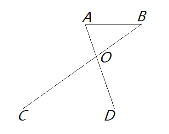
①已知:如图,AB∥CD。AD与BC相交于点O,试说明△ABO∽△DCO。
②已知:如图,在△ABC中,点D、E、F分别在边BC、AB、AC上,∠B=∠C=∠EDF,试说明△BDE∽△CFD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一块等腰直角的三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C的位置,使A、C、B′三点共线,那么旋转角度的大小为( )
A.45°
B.90°
C.120°
D.135°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com