
分析 (1)原式第一项利用绝对值的代数意义化简,第二项利用乘法分配律计算,第三项利用负整数指数幂法则计算,最后一项利用特殊角的三角函数值计算即可得到结果;
(2)原式利用除法法则变形,约分得到最简结果,把m与n的值代入计算即可求出值.
解答 解:(1)原式=$\sqrt{3}$+4-3+$\frac{\sqrt{3}}{3}$-$\frac{\sqrt{3}}{3}$=$\sqrt{3}$+1;
(2)原式=-$\frac{(m+4)(m-4)}{(m+2)^{2}}$•$\frac{2n(m+2)}{m-4}$•$\frac{m(m+2)}{m+4}$=-2mn,
当m=2,n=-$\sqrt{3}$时,原式=4$\sqrt{3}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
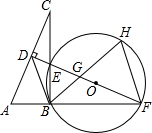 如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相较于点D,E,F,且BF=BC,⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交⊙O于点H,连接BD,FH.
如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相较于点D,E,F,且BF=BC,⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交⊙O于点H,连接BD,FH.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a-b)2=a2-b2 | B. | (-1+a)(-1-a)=a2-1 | C. | (2a)2÷a=2a | D. | -3a÷$\frac{1}{a}$×a=-3a3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com