
【题目】对于任意一个四位数,我们可以记为![]() ,即
,即![]() .若规定: 对四位正整数
.若规定: 对四位正整数![]() 进行 F运算,得到整数
进行 F运算,得到整数![]() .例如,
.例如,![]() ;
;![]() .
.
(1)计算:![]() ;
;
(2)当![]() 时,证明:
时,证明:![]() 的结果一定是4的倍数;
的结果一定是4的倍数;
(3)求出满足![]() 的所有四位数.
的所有四位数.
 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
【题目】央视举办的《中国诗词大会》受到广大学生群体广泛关注.某校的诗歌朗诵社团就《中国诗词大会》节目的喜爱程度,在校内对部分学生进行了问卷调查,并对问卷调查的结果分为“非常喜欢”、“比较喜欢”、“感觉一般”、“不太喜欢”四个等级,分别记作A、B、C、D.根据调查结果绘制出如图所示的扇形统计图和条形统计图,请结合图中说给信息解答下列问题:
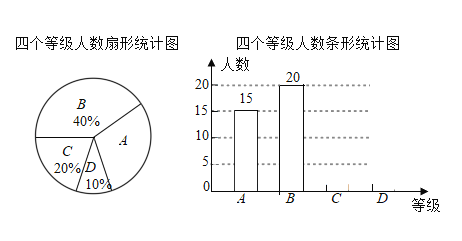
(1)本次被调查对象共有 人,扇形统计图中被调查者“非常喜欢”等级所对应圆心角的度数为 ;
(2)将条形统计图补充完整,并标明数据;
(3)若选“不太喜欢”的人中有两名女生,其余是男生,从原“不太喜欢”的人中挑选两名学生了解不太喜欢的原因,请用画树状图或列表法求所选取的这两名学生恰好是一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边长为20cm,∠ABC=120°.动点P、Q同时从点A出发,其中P以4cm/s的速度,沿A→B→C的路线向点C运动;Q先以2![]() cm/s的速度沿A→O的路线向点O运动,然后再以2cm/s的速度沿O→D的路线向点D运动,当P、Q到达终点时,整个运动随之结束,设运动时间为t秒.
cm/s的速度沿A→O的路线向点O运动,然后再以2cm/s的速度沿O→D的路线向点D运动,当P、Q到达终点时,整个运动随之结束,设运动时间为t秒.
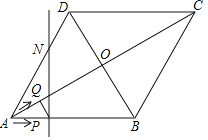
(1)在点P在AB上运动时,判断PQ与对角线AC的位置关系,并说明理由;
(2)若点Q关于菱形ABCD的对角线交点O的对称点为M,过点P且垂直于AB的直线l交菱形ABCD的边AD(或CD)于点N.
①直接写出当△PQM是直角三角形时t的取值范围;
②是否存在这样的t,使△PMN是以PN为一直角边的直角三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某养猪场对猪舍进行喷药消毒.在消毒的过程中,先经过![]() 的药物集中喷洒,再封闭猪舍
的药物集中喷洒,再封闭猪舍![]() ,然后再打开窗户进行通风.已知室内每立方米空气中含药量
,然后再打开窗户进行通风.已知室内每立方米空气中含药量![]() (
(![]() )与药物在空气中的持续时间
)与药物在空气中的持续时间![]() (
(![]() )之间的函数图象如图所示,其中在打开窗户通风前
)之间的函数图象如图所示,其中在打开窗户通风前![]() 与
与![]() 分别满足两个一次函数,在通风后
分别满足两个一次函数,在通风后![]() 与
与![]() 满足反比例函数.
满足反比例函数.
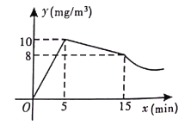
(1)求反比例函数的关系式;
(2)当猪舍内空气中含药量不低于![]() 且持续时间不少于
且持续时间不少于![]() ,才能有效杀死病毒,问此次消毒是否有效?
,才能有效杀死病毒,问此次消毒是否有效?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】滴滴快车是一种便捷的出行工具,某地的计价规则如表:
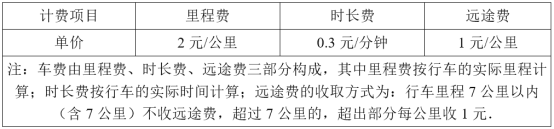
小李与小张分别从不同地点,各自同时乘坐滴滴快车,到同一地点相见,已知到达约定地点时他们的实际行车里程分别为7公里与9公里,两人付给滴滴快车的乘车费相同.其中一人先到达约定地点,他等候另一人的时间等于他自己实际乘车时间,且恰好是另一人实际乘车时间的一半,则小李的乘车费为_____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A1的坐标为(1,0),A2在y轴的正半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交x轴于点A3,过点A3作A3A4⊥A2A3,垂足为A3,交y轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交x轴于点A5;过点A5作A5A6⊥A4A5,垂足为A5,交y轴于点A6;…按此规律进行下去,则点A2020的横坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某便利店的咖啡单价为10元/杯,为了吸引顾客,该店共推出了三种会员卡,如下表:
会员卡类型 | 办卡费用/元 | 有效期 | 优惠方式 |
A类 | 40 | 1年 | 每杯打九折 |
B类 | 80 | 1年 | 每杯打八折 |
C类 | 130 | 1年 | 一次性购买2杯,第二杯半价 |
例如,购买A类会员卡,1年内购买50次咖啡,每次购买2杯,则消费![]() 元.若小玲1年内在该便利店购买咖啡的次数介于75~85次之间,且每次购买2杯,则最省钱的方式为( )
元.若小玲1年内在该便利店购买咖啡的次数介于75~85次之间,且每次购买2杯,则最省钱的方式为( )
A.购买A类会员卡B.购买B类会员卡
C.购买C类会员卡D.不购买会员卡
查看答案和解析>>
科目:初中数学 来源: 题型:
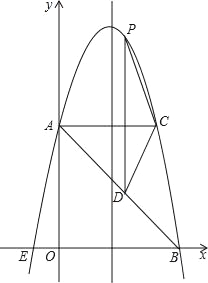
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E、B.
(1)求二次函数y=ax2+bx+c的表达式;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积;
(3)若点M在抛物线上,点N在其对称轴上,使得以A、E、N、M为顶点的四边形是平行四边形,且AE为其一边,求点M、N的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com