【题目】如图，DE⊥AB于E，DF⊥AC于F，若BD＝CD，BE＝CF.
(1)求证：AD平分∠BAC；
(2)猜想写出AB＋AC与AE之间的数量关系并给予证明．
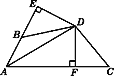
【答案】（1）证明见解析；（2）AB＋AC＝2AE.证明见解析.
【解析】试题分析：(1)、根据垂直得出△BDE与△CDE均为直角三角形，然后根据BD=CD，BE=CF得出三角形全等，从而得出DE=DF，根据角平分线的逆定理得出答案；(2)、根据角平分线得出∠EAD=∠CAD，结合∠E=∠AFD=90°得出∠ADE=∠ADF，从而说明△AED≌△AFD，根据全等得出AE=AF，最后根据AB+AC=AE﹣BE+AF+CF得出答案.
试题解析：(1)、∵DE⊥AB于E，DF⊥AC于F， ∴∠E=∠DFC=90°，∴△BDE与△CDE均为直角三角形，
∵
，∴△BDE≌△CDF， ∴DE=DF，即AD平分∠BAC；
、AB+AC=2AE．
科目：初中数学 来源： 题型：
【题目】求两个正整数的最大公约数是常见的数学问题，中国古代数学专著《九章算术》中便记载了求两个正整数最大公约数的一种方法﹣﹣更相减损术，术曰：“可半者半之，不可半者，副置分母、子之数，以少成多，更相减损，求其等也．以等数约之”，意思是说，要求两个正整数的最大公约数，先用较大的数减去较小的数，得到差，然后用减数与差中的较大数减去较小数，以此类推，当减数与差相等时，此时的差（或减数）即为这两个正整数的最大公约数．
例如：求91与56的最大公约数
解：
请用以上方法解决下列问题：
（1）求108与45的最大公约数；
（2）求三个数78、104、143的最大公约数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，现有一个面积为150平方米的长方形养鸡场，鸡场的一边靠墙（墙长18米），另三边用竹篱笆围成，在与墙平行的一边，开一扇2米宽的门.如果竹篱笆的长为33米，求这个长方形养鸡场与墙垂直的边长是多少？与墙平行的边长是多少？（列方程解答）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为参加重庆市校园足球开幕式，某学校老师欲给演出学生租用男、女演出服装若干套以供开幕式伴舞用．已知5套男装和8套女装租用一天共需租金510元，6套男装和10套女装租用一天共需630元
（1）租用男装、女装一天的价格分别是多少？
（2）该节目原计划由6名男同学和17名女同学完成，后因节目需要，将其中3名女同学由伴舞角色转向歌手角色，歌手服装每套租用一天的价格比已选定女装价格贵20%，求在演出当天租用服装实际需支付租金多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图①，我们在“格点”直角坐标系上可以看到，要求AB或CD的长度，可以转化为求Rt△ABC或Rt△DEF的斜边长．
例如：从坐标系中发现：D（﹣7，3），E（4，﹣3），所以DF=|5﹣（﹣3）|=8，EF=|4﹣（﹣7）|=11，所以由勾股定理可得：DE=
．
（1）在图①中请用上面的方法求线段AB的长：AB= ；
（2）在图②中：设A（x1，y1），B（x2，y2），试用x1，x2，y1，y2表示：AC= ，BC= ，AB= ；
（3）试用（2）中得出的结论解决如下题目：已知：A（2，1），B（4，3）；
①直线AB与x轴交于点D，求线段BD的长；
②C为坐标轴上的点，且使得△ABC是以AB为边的等腰三角形，请求出C点的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在等边三角形ABC的外侧作直线AP，点C关于直线AP的对称点为点D，连接AD，BD，其中BD交直线AP于点E.
（1）依题意补全图形；（2）若∠PAC＝20°，求∠AEB的度数；
（3）连结CE，写出AE, BE, CE之间的数量关系，并证明你的结论．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】把一副三角板按如图放置，其中∠ABC=∠DEB=90°，∠A=45°，∠D=30°，斜边AC=BD=10，若将三角板DEB绕点B逆时针旋转45°得到△D′E′B，则点A在△D′E′B的（ ） 
A.内部
B.外部
C.边上
D.以上都有可能
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】甲、乙两名射击运动员在某次训练中各射击10发子弹，成绩如表：
甲 | 8 | 9 | 7 | 9 | 8 | 6 | 7 | 8 | 10 | 8 |
乙 | 6 | 7 | 9 | 7 | 9 | 10 | 8 | 7 | 7 | 10 |
且 
=8，S乙2=1.8，根据上述信息完成下列问题：
（1）将甲运动员的折线统计图补充完整；
（2）乙运动员射击训练成绩的众数是 ， 中位数是 ．
（3）求甲运动员射击成绩的平均数和方差，并判断甲、乙两人本次射击成绩的稳定性．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
