
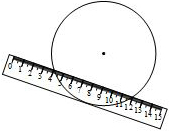
 如图,两边平行的刻度尺在圆上移动,当刻度尺的一边与直径为10cm的圆相切时,另一边与圆两个交点处的读数恰好为“4”和“12”(单位:cm),则刻度尺的宽为2cm.
如图,两边平行的刻度尺在圆上移动,当刻度尺的一边与直径为10cm的圆相切时,另一边与圆两个交点处的读数恰好为“4”和“12”(单位:cm),则刻度尺的宽为2cm. 科目:初中数学 来源:2017届江苏省无锡市九年级下学期第一次模拟考试数学试卷(解析版) 题型:填空题
在平面直角坐标系中,点O为坐标原点,A、B、C三点的坐标为( ,0)、(3
,0)、(3 ,0)、(0,5),点D在第一象限,且∠ADB=60º,则线段CD的长的最小值为______.
,0)、(0,5),点D在第一象限,且∠ADB=60º,则线段CD的长的最小值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在⊙O中,AB是直径,CD是弦,AB⊥CD于点H,DC=AH,连接AD、AC,点F在弦AE上,连接DF、CF,∠DFE=∠CAH,∠CFE=∠CAD,CH=$\sqrt{37}$,则AF长为5.
如图,在⊙O中,AB是直径,CD是弦,AB⊥CD于点H,DC=AH,连接AD、AC,点F在弦AE上,连接DF、CF,∠DFE=∠CAH,∠CFE=∠CAD,CH=$\sqrt{37}$,则AF长为5.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 将1、$\sqrt{2}$、$\sqrt{3}$、$\sqrt{6}$按如图方式排列,若规定(m,n)表示第m排的第n个数,如(4,2)表示的数是 $\sqrt{6}$,则(5,4)与(18,15)表示的两数之积是2$\sqrt{3}$.
将1、$\sqrt{2}$、$\sqrt{3}$、$\sqrt{6}$按如图方式排列,若规定(m,n)表示第m排的第n个数,如(4,2)表示的数是 $\sqrt{6}$,则(5,4)与(18,15)表示的两数之积是2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
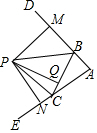 如图,∠DBC和∠ECB是△ABC的两个外角,点P是∠DBC、∠ECB两角的平分线的交点,PM、PN、PQ分别是P点到AB、AC、BC三边的垂线段,PM、PN、PQ的数量关系为( )
如图,∠DBC和∠ECB是△ABC的两个外角,点P是∠DBC、∠ECB两角的平分线的交点,PM、PN、PQ分别是P点到AB、AC、BC三边的垂线段,PM、PN、PQ的数量关系为( )| A. | PM>PN>PQ | B. | PM<PN<PQ | C. | PM=PN=PQ | D. | PM=PN>PQ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
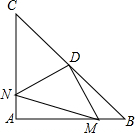 如图,在Rt△ABC中,AB=AC,∠BAC=90°,D为BC的中点.
如图,在Rt△ABC中,AB=AC,∠BAC=90°,D为BC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com