




 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源: 题型:
 (2012•顺义区二模)如图,小华同学设计了一个圆直径的测量器,把标有刻度的尺子OA、OB在O点钉在一起,并使它们保持互相垂直.在测直径时,把O点靠在圆周上,读得刻度OE=4个单位,OF=3个单位,则圆的直径为( )
(2012•顺义区二模)如图,小华同学设计了一个圆直径的测量器,把标有刻度的尺子OA、OB在O点钉在一起,并使它们保持互相垂直.在测直径时,把O点靠在圆周上,读得刻度OE=4个单位,OF=3个单位,则圆的直径为( )查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
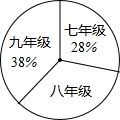 图,其中八年级学生人数为204人,请你根据图表中提供的信息,解答下列问题:
图,其中八年级学生人数为204人,请你根据图表中提供的信息,解答下列问题:| 图书种类 | 频数 | 频率 |
| 科普常识 | 840 | b |
| 名人传记 | 816 | 0.34 |
| 中外名著 | a | 0.25 |
| 其他 | 144 | 0.06 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com