Question

8．如图，在△ABC中，∠C=90°，AD平分∠BAC．
（1）当∠B=40°时，求∠ADC的度数；
（2）若AB=10cm，CD=4cm，求△ABD的面积．

Answer 1

分析 （1）根据三角形的内角和得到∠BAC=50°，根据三角形的外角的性质即可得到结论；
（2）过D作DE⊥AB于E，根据角平分线的性质得到DE=CD=4，由三角形的面积公式即可得到结论．

解答 解：（1）∵∠C=90°，∠B=40°，
∴∠BAC=50°，
∵AD平分∠BAC，
∴$∠BAD=∠DAC=\frac{1}{2}∠BAC=25°$，
∴∠ADC=∠B+∠BAD=65°；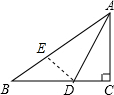
（2）过D作DE⊥AB于E，
∵AD平分∠BAC，
∴DE=CD=4，
∴S${\;}_{△ABD=\frac{1}{2}}$AB•DE=$\frac{1}{2}$×10×4=20cm²．

点评 本题考查了三角形的内角和，三角形的面积的计算，角平分线的性质，熟练掌握角平分线的性质是解题的关键．