
【题目】如图,菱形ABCD中,AB=3,E是BC上一个动点(不与点B、C重合),EF∥AB,交BD于点G,设BE=x,△GED的面积与菱形ABCD的面积之比为y,则y与x的函数图象大致为( )
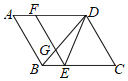
A. B.
B.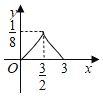 C.
C.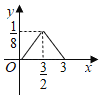 D.
D.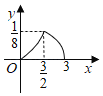
【答案】A
【解析】
连接BF,求出平行四边形ABEF与平行四边形ABCD的面积关系,再求得△BEF与△BEF的面积关系,进而得△BDE与平行四边形ABCD的面积的关系,再证明△GBE∽△GDF,得出GE:GF,进而得△BEG与△BEF的面积关系,最后得y与x的关系式,根据函数关系式确定函数图象.
解:连接BF,

∵四边形ABCD是菱形,AB=3,
∴AD∥BC,AB=BC=CD=AD=3,
∵EF∥AB,
∴四边形ABEF是平行四边形,
∴AF=BE=x,
∴![]() =,
=,
∵AD∥BC,
∴△GBE∽△GDF,
∴![]() ,
,
∴![]() ,
,
∵AD∥BC,
∴![]() ,
,
∴S△GED=S△BED﹣S△BEG=![]() =
=![]() ,
,
∴![]() ,
,
即y=![]() (0<x<3),
(0<x<3),
∵![]() ,
,
∴y=![]() (0<x<3)是开口向下的抛物线,
(0<x<3)是开口向下的抛物线,
故选:A.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
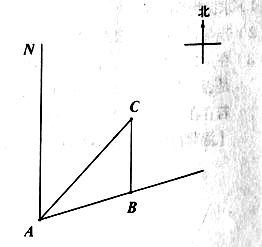
【题目】如图,一艘船以每小时30海里的速度向北偏东75°方向航行,在点![]() 处测得码头
处测得码头![]() 的船的东北方向,航行40分钟后到达
的船的东北方向,航行40分钟后到达![]() 处,这时码头
处,这时码头![]() 恰好在船的正北方向,在船不改变航向的情况下,求出船在航行过程中与码头
恰好在船的正北方向,在船不改变航向的情况下,求出船在航行过程中与码头![]() 的最近距离.(结果精确的0.1海里,参考数据
的最近距离.(结果精确的0.1海里,参考数据![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,∠BAC=20°,点O是AB的中点,将OB绕点O顺时针旋转α角时(0°<α<180°),得到OP,当△ACP为等腰三角形时,α的值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AD、BD分别是![]() 的内角∠BAC、∠ABC的平分线,过点A作AE⊥AD,交BD的延长线于点E.
的内角∠BAC、∠ABC的平分线,过点A作AE⊥AD,交BD的延长线于点E.

(1)求证:![]() ;
;
(2)如图2,如果AE=AB,且BD:DE=2:3,求BC:AB的值;
(3)如果∠ABC是锐角,且![]() 与
与![]() 相似,求∠ABC的度数,并直接写出
相似,求∠ABC的度数,并直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明调查了本校九年级300名学生到校的方式,根据调査结果绘制出统计图的一部分如图:
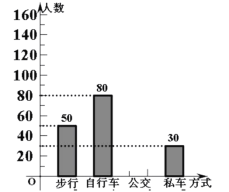
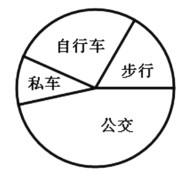
(1)补全条形统计图;
(2)求扇形统计图中表示“步行”的扇形圆心角的度数;
(3)请估计在全校1200名学生中乘公交的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
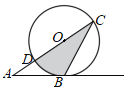
【题目】如图,⊙O的圆心O在△ABC的边AC上,AC与⊙O分别交于C,D两点,⊙O与边AB相切,且切点恰为点B.
(1)求证:∠A+2∠C=90°;
(2)若∠A=30°,AB=6,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司计划购买A,B两种型号的机器人搬运材料.已知A型机器人比B型机器人每小时多搬运30kg材料,且A型机器人搬运1000kg材料所用的时间与B型机器人搬运800kg材料所用的时间相同.
(1)求A,B两种型号的机器人每小时分别搬运多少材料;
(2)该公司计划采购A,B两种型号的机器人共20台,要求每小时搬运材料不得少于2800kg,则至少购进A型机器人多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
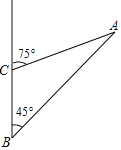
【题目】青白江凤凰湖湿地公园是一处具有国际水准的旅游度假区,以生态、休闲、水景环境及具有多国风情的建筑为特色.如图为凤凰湖湿地公园三个景点A,B,C的平面示意图,景点C在B的正北方向4千米处,景点A在B的东北方向,在C的北偏东75°方向上,求景点A、B之间的距离.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点D在AB的延长线上,C、E是⊙O上的两点,CE=CB,∠BCD=∠CAE,延长AE交BC的延长线于点F.
(1)求证:CD是⊙O的切线;
(2)求证:CE=CF;
(3)若BD=1,CD=![]() ,求弦AC的长.
,求弦AC的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com