
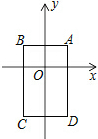
 如图,在平面直角坐标系中,已知点A(1,1),B(-1,1),C(-1,-2),D(1,-2),把一根长为2017个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在A处,并按A→B→C→D→A→…的规律紧绕在四边形ABCD的边上.则细线的另一端所在位置的点的坐标是(1,-2).
如图,在平面直角坐标系中,已知点A(1,1),B(-1,1),C(-1,-2),D(1,-2),把一根长为2017个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在A处,并按A→B→C→D→A→…的规律紧绕在四边形ABCD的边上.则细线的另一端所在位置的点的坐标是(1,-2). 分析 根据点A、B、C、D的坐标可得出AB、BC的长度以及四边形ABCD为矩形,进而可求出矩形ABCD的周长,根据细线的缠绕方向以及细线的长度即可得出细线的另一端所在位置,此题得解.
解答 解:∵A(1,1),B(-1,1),C(-1,-2),D(1,-2),
∴AB=CD=2,AD=BC=3,且四边形ABCD为矩形,
∴矩形ABCD的周长C矩形ABCD=2(AB+BC)=10.
∵2017=201×10+7,AB+BC+CD=7,
∴细线的另一端落在点D上,即(1,-2).
故答案为(1,-2).
点评 本题考查了规律型中点的坐标、矩形的判定以及矩形的周长,根据矩形的周长结合细线的长度找出细线终点所在的位置是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
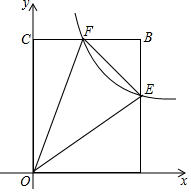 如图在矩形OABC中,OA=5,OC=6,反比例函数的图象与AB、BC分别交于点E、F,且AE<EB,△OEF与△BEF的面积之差等于5$\frac{11}{30}$,求此反比例函数的解析式.
如图在矩形OABC中,OA=5,OC=6,反比例函数的图象与AB、BC分别交于点E、F,且AE<EB,△OEF与△BEF的面积之差等于5$\frac{11}{30}$,求此反比例函数的解析式.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com