
【题目】台风是一种自然灾害,它以台风中心为圆心,在周围数十千米范围内形气旋风暴,有极强的破坏力,此时某台风中心在海域B处,在沿海城市A的正南方向240千米,其中心风力为12级,每远离台风中心25千米,台风就会减弱一级,如图所示,该台风中心正以20千米/时的速度沿北偏东30°方向向C移动,且台风中心的风力不变,若城市所受风力达到或超过4级,则称受台风影响. 试问:

(1)A城市是否会受到台风影响?请说明理由.
(2)若会受到台风影响,那么台风影响该城市的持续时间有多长?
(3)该城市受到台风影响的最大风力为几级?
【答案】(1)该城市会受到这次台风的影响;(2)16;(3)7.2.
【解析】
试题(1)过A作AD⊥BC于D,利用30°角所对边是斜边一半,求得AD,与200比较.(2) 以A为圆心,200为半径作⊙A交BC于E、F,勾股定理计算弦长EF.(3) AD距台风中心最近,计算风力级别.
试题解析:
(1)该城市会受到这次台风的影响. 理由是:如图,过A作AD⊥BC于D.在Rt△ABD中,
∵∠ABD=30°,AB=240,
∴AD= ![]() AB=120,
AB=120,
∵城市受到的风力达到或超过四级,则称受台风影响,
∴受台风影响范围的半径为25×(12﹣4)=200,
∵120<200,
∴该城市会受到这次台风的影响.
(2)如图以A为圆心,200为半径作⊙A交BC于E、F, 则AE=AF=200,
∴台风影响该市持续的路程为:EF=2DE=2 ![]() =320,
=320,
∴台风影响该市的持续时间t=320÷20=16(小时).
(3)∵AD距台风中心最近,
∴该城市受到这次台风最大风力为:12﹣(120÷25)=7.2(级).



科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A=30°,沿BE将此三角形对折,又沿BA′再一次对折,点C落在BE上的C′处,此时∠C′DB=84°,则∠![]() EA度数为( )
EA度数为( )
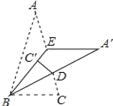
A.54°B.81°C.108°D.114°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,D是直线BC上一点(不与点B、C重合),以AD为一边在AD的右侧作△ADE,AD=AE,∠DAE=∠BAC,连接CE.
(1)如左下图,当点D在线段BC上时,写出△ABD≌△ACE的理由;
(2)如下中图,当点D在线段BC上,∠BAC=90°,直接写出∠BCE的度数;
(3)如右下图,若∠BCE=α,∠BAC=β.点D在线段CB的延长线上时,则α、β之间有怎样的数量关系?写出你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知MB=ND,∠MBA=∠NDC,下列哪个条件不能判定△ABM≌△CDN( )

A.AM=CNB.AB=CD C.AM∥CN D.∠M=∠N
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把Rt△ABC放在平面直角坐标系内,其中∠CAB=90°,BC=5,点A,B的坐标分别为(1,0),(4,0),将△ABC沿![]() 轴向右平移,当点C落在直线
轴向右平移,当点C落在直线![]() 上时,线段BC扫过的面积为( )
上时,线段BC扫过的面积为( )
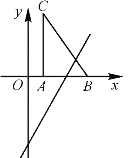
A. 16B. 8C. 8![]() D. 4
D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知A,B是抛物线y=ax2(a>0)上两个不同的点,其中A在第二象限,B在第一象限.
(1)如图1所示,当直线AB与x轴平行,∠AOB=90°,且AB=2时,求此抛物线的解析式和A,B两点的横坐标的乘积;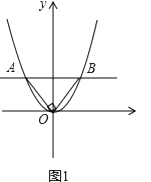
(2)如图2所示,在(1)所求得的抛物线上,当直线AB与x轴不平行,∠AOB仍为90°时,求证:A、B两点横坐标的乘积是一个定值;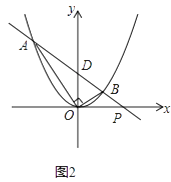
(3)在(2)的条件下,如果直线AB与x轴、y轴分别交于点P、D,且点B的横坐标为 ![]() .那么在x轴上是否存在一点Q,使△QDP为等腰三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
.那么在x轴上是否存在一点Q,使△QDP为等腰三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为降低空气污染,启东飞鹤公交公司决定全部更换节能环保的燃气公交车.计划购买A型和B型两种公交车共10辆,其中每台的价格,年载客量如表:
A型 | B型 | |
价格(万元/台) | a | b |
年载客量(万人/年) | 60 | 100 |
若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.
(1)求a,b的值;
(2)如果该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次.请你设计一个方案,使得购车总费用最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一张如图1的长方形铁皮,四个角都剪去边长为![]() 的正方形,再四周折起,做成一个有底无盖的铁盒如图2,铁盒底面长方形的长是
的正方形,再四周折起,做成一个有底无盖的铁盒如图2,铁盒底面长方形的长是![]() ,宽是
,宽是![]() 这个无盖铁盒各个面的面积之和称为铁盒的全面积.
这个无盖铁盒各个面的面积之和称为铁盒的全面积.

(1)图1中原长方形铁皮的面积为_![]() ;(用
;(用![]() 的代数式表示)
的代数式表示)
(2)若要在铁盒的各个外表面漆上某种油漆,每元钱可涂的面积为![]() ,则涂完这个铁盒需要多少钱?(用
,则涂完这个铁盒需要多少钱?(用![]() 的代数式表示)
的代数式表示)
(3)是否存在一个最大正整数![]() ,使得铁盒的全面积是底面积的正整数倍?若存在,请直接写出这个
,使得铁盒的全面积是底面积的正整数倍?若存在,请直接写出这个![]() ,若不存在,请说明理由.
,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com