
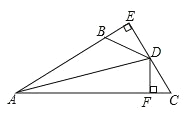
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF,
(1)求证:AD平分∠BAC;(2)已知AC=20, BE=4,求AB的长.
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:
【题目】我市某中学有一块四边形的空地ABCD,如图所示,为了绿化环境,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,DA=4m,BC=12m,CD=13m.
(1)求出空地ABCD的面积.
(2)若每种植1平方米草皮需要200元,问总共需投入多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
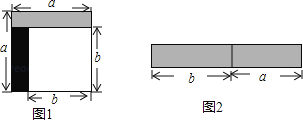
【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)上述操作能验证的等式是 ;(请选择正确的一个)
A、a2﹣2ab+b2=(a﹣b)2 B、a2﹣b2=(a+b)(a﹣b) C、a2+ab=a(a+b)
(2)应用你从(1)选出的等式,完成下题:
计算:(1﹣![]() )(1﹣
)(1﹣![]() )(1﹣
)(1﹣![]() )…(1﹣
)…(1﹣![]() )(1﹣
)(1﹣![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们来定义一种新运算:对于任意实数x、y,“※”为a※b=(a+1)(b+1)﹣1
(1)计算(﹣3)※9
(2)嘉琪研究运算“※”之后认为它满足交换律,你认为她的判断 (正确、错误)
(3)请你帮助嘉琪完成她对运算“※”是否满足结合律的证明.
证明:由已知把原式化简得a※b=(a+1)(b+1)﹣1=ab+a+b
∵(a※b)※c=(ab+a+b)※c=
a※(b※c)=
∴
∴运算“※”满足结合律.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE交AE延长线于D,DM⊥AC交AC的延长线于M,连接CD,以下四个结论:

①∠ADC=45°;②BD=![]() AE;③AC+CE=AB;④AC+AB=2AM.其中正确的结论有( )
AE;③AC+CE=AB;④AC+AB=2AM.其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两种型号的机器加工同一种零件,已知A型机器比B型机器每小时多加工20个零件,A型机器加工400个零件所用时间与B型机器加工300个零件所用时间相同.A型机器每小时加工零件的个数_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某校有一长方形操场,长为x m,宽为y m,为了美化校园环境,学校决定在操场四周修建m m宽的绿化带,负责后勤的王老师让八年级某班学生计算一下剩下操场的面积,可是该班学生计算出了两种结果:一种是(xy-2mx-2my)m2,另一种是(xy-2mx-2my+4m2)m2,并且为此争论不休,作为一名八年级学生,你能运用所学的知识来帮助他们判断对错吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B、D、E在⊙O上,弦AE、BD的延长线相交于点C.若AB是⊙O的直径,D是BC的中点. 
(1)试判断AB、AC之间的大小关系,并给出证明;
(2)在上述题设条件下,当△ABC为正三角形时,点E是否AC的中点?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了帮助市内一名患“白血病”的中学生,东营市某学校数学社团15名同学积极捐款,捐款情况如下表所示,下列说法正确的是( )
捐款数额 | 10 | 20 | 30 | 50 | 100 |
人数 | 2 | 4 | 5 | 3 | 1 |
A. 众数是100 B. 中位数是30 C. 极差是20 D. 平均数是30
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com