
 ��ͼ����֪������T��y=ax2+bx+c��a��0����x�ύ��A��B���㣨��A��x����������ϣ�����y�ύ�ڵ�C������DEFG��һ����DE���߶�AB�ϣ�����F��G�ֱ����߶�BC��AC�ϣ�������T�ϲ��ֵ�ĺ������Ӧ�����������£�
��ͼ����֪������T��y=ax2+bx+c��a��0����x�ύ��A��B���㣨��A��x����������ϣ�����y�ύ�ڵ�C������DEFG��һ����DE���߶�AB�ϣ�����F��G�ֱ����߶�BC��AC�ϣ�������T�ϲ��ֵ�ĺ������Ӧ�����������£�| x | �� | -3 | -2 | 1 | 2 | �� |
| y | �� | -$\frac{5}{2}$ | -4 | -$\frac{5}{2}$ | 0 | �� |
���� ��1������ͼ�����Եõ��������߾������ĵ�����꣬���ݴ���ϵ������������������������y=ax2+bx+c��a��0���Ϳ��Խ�ú����Ľ���ʽ�������Ϳ������A��B��C�����꣮
��2����֤��ADG�ס�AOC��AD=2-m���������������εĶ�Ӧ�ߵı���ȣ��Ϳ�����m��ʾ��DG�ij����ٸ��ݡ�BEF�ס�BOC���Ϳ��Ա�ʾ��BE���Ϳ��Եõ�OE�����ED�Ϳ��Ա�ʾ���������S��m�ĺ�����ϵ�Ϳ��Եõ���
��3��������DEFG�����Sȡ���ֵʱ�����Ǻ�����ֵ�����ֵʱ�����ݶ��κ��������ʾͿ��������Ӧ��m��ֵ��
�ٸ���S��PBC=m=1�õ�P��BC�ľ���Ϊ$\frac{\sqrt{2}}{4}$�����Եõ�ƽ����BC�ҵ�BC�ľ���Ϊ$\frac{\sqrt{2}}{4}$�Ľ���ʽ�������������߽���ʽ���ɵõ�P�����ꣻ
�ھ��ε��ĸ����������Ϳ�����������ݴ���ϵ�����Ϳ������ֱ��DF�Ľ���ʽ���Ϳ������ֱ��DF�������ߵĽ�������꣬����FM=k•DF���Ϳ��Ա�ʾ��M�����꣬��M��������뺯���Ϳ��Եõ�һ������k�ķ��̣����k��ֵ���ж��Ƿ����㺯���Ľ���ʽ��
��� �⣺��1���ⷨһ����y=ax2+bx+c��a��0����
��ȡx��y������ֵ���룬�������ʽy=$\frac{1}{2}$x2+x-4��
��y=0�����x1=-4��x2=2��
��x=0����y=-4��
��A��B��C���������ֱ���A��2��0����B��-4��0����C��0��-4����
�ⷨ������������P���㣨1��-$\frac{5}{2}$������-3��-$\frac{5}{2}$����֪��
������P�ĶԳ��᷽��Ϊx=-1��
�֡�������P����2��0������-2��-4����
���������ߵĶԳ��Կ�֪��
��A��B��C������ֱ�ΪA��2��0����B��-4��0����C��0��-4����
��2�������⣬$\frac{AD}{AO}$=$\frac{DG}{OC}$����AO=2��OC=4��AD=2-m����DG=4-2m��
��$\frac{BE}{BO}$=$\frac{EF}{OC}$��EF=DG����BE=4-2m��
��DE=3m��
��SDEFG=DG•DE=��4-2m��3m=12m-6m2��0��m��2����
��3����SDEFG=12m-6m2��0��m��2����
��m=1ʱ�����ε�����������������6��
��S��PBC=m=1��
P��BC�ľ���Ϊ$\frac{\sqrt{2}}{4}$��
��ƽ����BC�ҵ�BC�ľ���Ϊ$\frac{\sqrt{2}}{4}$�Ľ���ʽΪy=-x-$\frac{9}{2}$��y=-x-$\frac{7}{2}$��
���������߽���ʽ��
$\left\{\begin{array}{l}{y=-x-\frac{9}{2}}\\{y=\frac{1}{2}{x}^{2}+x-4}\end{array}\right.$�����$\left\{\begin{array}{l}{{x}_{1}=-2-\sqrt{3}}\\{{y}_{1}=-\frac{5}{2}+\sqrt{3}}\end{array}\right.$��$\left\{\begin{array}{l}{{x}_{2}=-2+\sqrt{3}}\\{{y}_{2}=-\frac{5}{2}-\sqrt{3}}\end{array}\right.$��
��$\left\{\begin{array}{l}{y=-x-\frac{7}{2}}\\{y=\frac{1}{2}{x}^{2}+x-4}\end{array}\right.$�����$\left\{\begin{array}{l}{{x}_{3}=-2-\sqrt{5}}\\{{y}_{3}=-\frac{3}{2}+\sqrt{5}}\end{array}\right.$��$\left\{\begin{array}{l}{{x}_{4}=-2+\sqrt{5}}\\{{y}_{4}=-\frac{3}{2}-\sqrt{5}}\end{array}\right.$��
��P��������-2-$\sqrt{3}$��-$\frac{5}{2}$+$\sqrt{3}$����-2+$\sqrt{3}$��-$\frac{5}{2}$-$\sqrt{3}$����-2-$\sqrt{5}$��-$\frac{3}{2}$+$\sqrt{5}$����-2+$\sqrt{5}$��-$\frac{3}{2}$-$\sqrt{5}$����
�ڵ�����������ʱ���䶥��ΪD��1��0����G��1��-2����F��-2��-2����E��-2��0����
��ֱ��DF�Ľ���ʽΪy=kx+b����֪k=$\frac{2}{3}$��b=-$\frac{2}{3}$�� ��y=$\frac{2}{3}$x-$\frac{2}{3}$��
��y=$\frac{2}{3}$x-$\frac{2}{3}$��
�ֿ����������P�Ľ���ʽΪ��y=$\frac{1}{2}$x2+x-4��
��$\frac{2}{3}$x-$\frac{2}{3}$=$\frac{1}{2}$x2+x-4�������x=$\frac{-1��\sqrt{61}}{3}$��
��ͼ��������DF��������P�ཻ�ڵ�N����N�ĺ�����Ϊ$\frac{-1-\sqrt{61}}{3}$����N��x��Ĵ��߽�x����H��
��$\frac{FN}{DF}$=$\frac{HE}{DE}$=$\frac{-2-\frac{-1-\sqrt{61}}{3}}{3}$=$\frac{-5+\sqrt{61}}{9}$��
��M����������P�ϣ�����M����N�غ�ʱ����ʱk��ȡֵ��Χ��k��$\frac{\sqrt{61}-5}{9}$��k��0��
���� ������Ҫ�����˶��κ����ۺ��⣬�漰����ϵ���������Ľ���ʽ�����ú����Ľ���ʽ��ɵķ�����������������ķ��������������ε����ʣ��ۺ��Խ�ǿ���ѶȽϴ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У���ACB=90�㣬AC=BC��BC��y�ύ��D�㣬��C������Ϊ��-1��0������A������Ϊ��-5��2������D��������ǣ�0��2����
��ͼ���ڡ�ABC�У���ACB=90�㣬AC=BC��BC��y�ύ��D�㣬��C������Ϊ��-1��0������A������Ϊ��-5��2������D��������ǣ�0��2�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
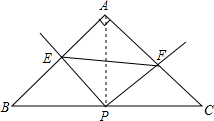 ��ͼ�⣬�ڡ�ABC�У�AB=AC����BAC=90�㣬ֱ��EPF�Ķ���P��BC���е㣬����PE��PF�ֱ�AB��AC�ڵ�E��F
��ͼ�⣬�ڡ�ABC�У�AB=AC����BAC=90�㣬ֱ��EPF�Ķ���P��BC���е㣬����PE��PF�ֱ�AB��AC�ڵ�E��F�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��һֻ�����Ծ��ȵ��ٶ���̨��A��B��C��D��E���У���ô�������еĸ߶�h��ʱ��t�ĺ���ͼ������ǣ�������
��ͼ��һֻ�����Ծ��ȵ��ٶ���̨��A��B��C��D��E���У���ô�������еĸ߶�h��ʱ��t�ĺ���ͼ������ǣ�������| A�� |  | B�� |  | C�� | 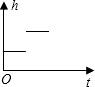 | D�� | 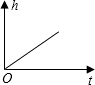 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
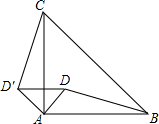 ��ͼ��D�ǵ���ֱ�ǡ�ABC��һ�㣬BC��б�ߣ��������ABD�Ƶ�A��ʱ�뷽����ת����ACD ��λ�ã�B��C�غϣ�D��D���غϣ������ADD��Ķ����ǣ�������
��ͼ��D�ǵ���ֱ�ǡ�ABC��һ�㣬BC��б�ߣ��������ABD�Ƶ�A��ʱ�뷽����ת����ACD ��λ�ã�B��C�غϣ�D��D���غϣ������ADD��Ķ����ǣ�������| A�� | 25�� | B�� | 30�� | C�� | 35�� | D�� | 45�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��AB�ǡ�Oֱ����OC��AB����CD��OB���ڵ�F������D��A�ֱ�����O�����߽��ڵ�G������GD��AB�ӳ��߽��ڵ�E��
��ͼ��AB�ǡ�Oֱ����OC��AB����CD��OB���ڵ�F������D��A�ֱ�����O�����߽��ڵ�G������GD��AB�ӳ��߽��ڵ�E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ���㽭ʡ������У�������꼶��ѧ�ڵ�һ���¿���ѧ�Ծ��������棩 ���ͣ���ѡ��
���м�����ȷ���ǣ��� ��
A.  ��
��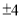 B.
B.  C.
C. 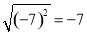 D.
D. 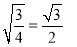
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com