
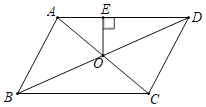
【题目】如图,□ABCD的对角线AC与BD相交于点O,过点O作OE⊥AD于点E,若AB=4,∠ABC=60°,则OE的长是( )
A.![]() B.2
B.2![]() C.2D.
C.2D.![]()
 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
【题目】如图,是某公园一圆形喷水池,在池中心竖直安装一根水管OA=1.25m,A处是喷头,水流在各个方向沿形状相同的抛物线落下,水落地后形成一个圆,圆心为O,直径为线段CB.建立如图所示的平面直角坐标系,若水流路线达到最高处时,到x轴的距离为2.25m,到y轴的距离为1m,则水落地后形成的圆的直径CB=_____m.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,y=ax2+bx+c的图象经过点(﹣1,0),(m,0);有如下判断:①abc<0;②b>3c;③![]() =1﹣
=1﹣![]() ;④|am+a|=
;④|am+a|=![]() .其中正确的判断有( )
.其中正确的判断有( )
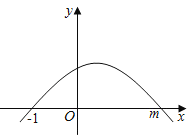
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
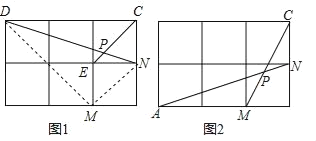
【题目】(问题呈现)如图1,在边长为1的正方形网格中,连接格点D,N和E,C,DN和EC相交于点P,求tan∠CPN的值.
(方法归纳)求一个锐角的三角函数值,我们往往需要找出(或构造出)一个直角三角形.观察发现问题中∠CPN不在直角三角形中,我们常常利用网格画平行线等方法解决此类问题,比如连接格点M,N,可得MN∥EC,则∠DNM=∠CPN,连接DM,那么∠CPN就变换到Rt△DMN中.
(问题解决)(1)直接写出图1中tan∠CPN的值为 ;
(2)如图2,在边长为1的正方形网格中,AN与CM相交于点P,求cos∠CPN的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
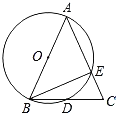
【题目】如图,AB是⊙O的直径,AB=AC,BC交⊙O于点D,∠BAC=45°,给出下列四个结论:①∠EBC=22.5°②BD=DC③AE=DC④![]() =2
=2![]() ,其中正确结论有_____(只填序号)
,其中正确结论有_____(只填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年4月23日是中国人民解放军海军成立70周年纪念日,届时将在青岛举行盛大的多国海军庆祝活动.为此我国海军进行了多次军事演习.如图,在某次军事演习时,舰艇A发现在他北偏东22°方向上有不明敌舰在指挥中心O附近徘徊,快速报告给指挥中心,此时在舰艇A正西方向50海里处的舰艇B接到返回指挥中心的行动指令,舰艇B迅速赶往在他北偏东60°方向的指挥中心处,舰艇B的速度是80海里/小时,请根据以上信息,求舰艇B到达指挥中心O的时间.(结果精确到0.1小时,参考数据:(sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,![]() =1.73)
=1.73)
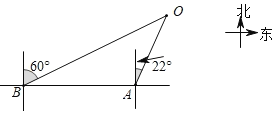
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,y=ax2+bx+c的图象经过点(﹣1,0),(m,0);有如下判断:①abc<0;②b>3c;③![]() =1﹣
=1﹣![]() ;④|am+a|=
;④|am+a|=![]() .其中正确的判断有( )
.其中正确的判断有( )
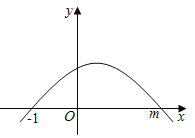
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com