
【题目】几何证明:
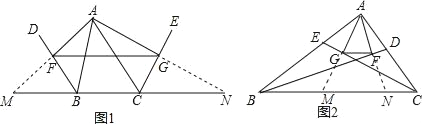
(1)已知:如图1,BD、CE分别是△ABC的外角平分线,过点A作AF⊥BD,AG⊥CE,垂足分别是F、G,连接FG,延长AF、AG,与直线BC相交.求证:FG=![]() (AB+BC+AC).
(AB+BC+AC).
(2)若BD、CE分别是△ABC的内角平分线,其余条件不变(如图1),线段FG与△ABC的三边又有怎样的数量关系?写出你的猜想,并给予证明.
【答案】(1)见解析;(2)线段FG与△ABC三边的数量关系是FG=![]() (AB+AC﹣BC),理由见解析
(AB+AC﹣BC),理由见解析
【解析】
(1)利用全等三角形的判定定理ASA证得△ABF≌△MBF,然后由全等三角形的对应边相等进一步推出MB=AB,AF=MF,同理CN=AC,AG=NG,由此可以证明FG为△AMN的中位线,然后利用中位线定理求得FG=![]() (AB+BC+AC);(2)延长AF、AG,与直线BC相交于M、N,与(1)类似可以证出答案.
(AB+BC+AC);(2)延长AF、AG,与直线BC相交于M、N,与(1)类似可以证出答案.
(1)如图1,∵AF⊥BD,∠ABF=∠MBF,
∴∠BAF=∠BMF,
在△ABF和△MBF中,
∵ ,
,
∴△ABF≌△MBF(ASA)
∴MB=AB
∴AF=MF,
同理:CN=AC,AG=NG,
∴FG是△AMN的中位线
∴FG=![]() MN,
MN,
=![]() (MB+BC+CN),
(MB+BC+CN),
=![]() (AB+BC+AC).
(AB+BC+AC).
(2)图2中,FG=![]() (AB+AC﹣BC)
(AB+AC﹣BC)
理由如下:如图2,
延长AG、AF,与直线BC相交于M、N,
∵由(1)中证明过程类似证△ABF≌△NBF,
∴NB=AB,AF=NF,
同理CM=AC,AG=MG
∴FG=![]() MN,
MN,
∴MN=2FG,
∴BC=BN+CM﹣MN=AB+AC﹣2FG,
∴FG=![]() (AB+AC﹣BC),
(AB+AC﹣BC),
答:线段FG与△ABC三边的数量关系是FG=![]() (AB+AC﹣BC).
(AB+AC﹣BC).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】甲乙两件服装的进价共500元,商场决定将甲服装按30%的利润定价,乙服装按20%的利润定价,实际出售时,两件服装均按9折出售,商场卖出这两件服装共获利67元.
(1)求甲乙两件服装的进价各是多少元;
(2)由于乙服装畅销,制衣厂经过两次上调价格后,使乙服装每件的进价达到242元,求每件乙服装进价的平均增长率;
(3)若每件乙服装进价按平均增长率再次上调,商场仍按9折出售,定价至少为多少元时,乙服装才可获得利润(定价取整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好治理西太湖水质,保护环境,市治污公司决定购买10 台污水处理设备,现有A、B两种型号的设备,其中每台的价格,月处理污水量如下表:

经调查:购买-台A型设备比购买一-台B型设备多2万元,购买2台A型设备比购买4台B型设备少4万元.
(1)求a、b的值;
(2)经预算:市治污公司购买污水处理设备的资金不超过47万元,并且该月要求处理西太湖的污水量不低于1860 吨,则有哪几种购买方案?请指出最省钱的一种购买方案,并指出相应的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,O为直线AB上一点,过点O作射线OC,![]() ,将一直角三角板
,将一直角三角板![]() 的直角顶点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方.
的直角顶点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方.
![]() 将图1中的三角板绕点O以每秒
将图1中的三角板绕点O以每秒![]() 的速度沿逆时针方向旋转一周
的速度沿逆时针方向旋转一周![]() 如图2,经过t秒后,ON落在OC边上,则
如图2,经过t秒后,ON落在OC边上,则![]() ______秒
______秒![]() 直接写结果
直接写结果![]() .
.
![]() 如图2,三角板继续绕点O以每秒
如图2,三角板继续绕点O以每秒![]() 的速度沿逆时针方向旋转到起点OA上
的速度沿逆时针方向旋转到起点OA上![]() 同时射线OC也绕O点以每秒
同时射线OC也绕O点以每秒![]() 的速度沿逆时针方向旋转一周,
的速度沿逆时针方向旋转一周,
![]() 当OC转动9秒时,求
当OC转动9秒时,求![]() 的度数.
的度数.
![]() 运动多少秒时,
运动多少秒时,![]() ?请说明理由.
?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数 ![]() 的图象交于A(m,6),B(3,n)两点.
的图象交于A(m,6),B(3,n)两点. 
(1)求一次函数的解析式;
(2)根据图象直接写出 ![]() 的x的取值范围;
的x的取值范围;
(3)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动课上,某学习小组对有一内角为120°的平行四边形ABCD(∠BAD=120°)进行探究:将一块含60°的直角三角板如图放置在平行四边形ABCD所在平面内旋转,且60°角的顶点始终与点C重合,较短的直角边和斜边所在的两直线分别交线段AB,AD于点E,F(不包括线段的端点).
(1)初步尝试
如图1,若AD=AB,求证:①△BCE≌△ACF,②AE+AF=AC;
(2)类比发现
如图2,若AD=2AB,过点C作CH⊥AD于点H,求证:AE=2FH;
(3)深入探究
如图3,若AD=3AB,探究得: ![]() 的值为常数t,则t= .
的值为常数t,则t= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形ABCD中,两条对角线AC,BD相交于点O,∠MON+∠BCD=180°,∠MON绕点O旋转,射线OM交边BC于点E,射线ON交边DC于点F,连接EF.
(1)如图1,当∠ABC=90°时,△OEF的形状是;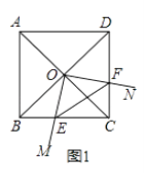
(2)如图2,当∠ABC=60°时,请判断△OEF的形状,并说明理由;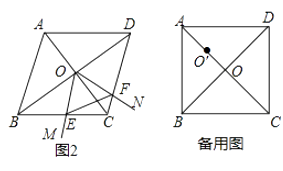
(3)在(1)的条件下,将∠MON的顶点移到AO的中点O′处,∠MO′N绕点O′旋转,仍满足∠MO′N+∠BCD=180°,射线O′M交直线BC于点E,射线O′N交直线CD于点F,当BC=4,且 ![]() =
= ![]() 时,直接写出线段CE的长.
时,直接写出线段CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲乙两人在游泳池A处发现游泳池中的P处有人求救,甲立即跳入池中去救人,速度为1米/秒,乙以3.5米/秒的速度沿游泳池边跑到距A不远处的B处,捡起一个游泳圈再跳入池中去救人,甲游了20秒到达P处,两秒后乙到达P处.若∠PAB与∠PBC互余,且cos∠PBC= ![]() ,求乙的游泳速度.
,求乙的游泳速度. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近期电视剧《人民的名义》热播,某校“话剧表演”社团在本校学生中开展学生知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A,B,C,D四类.其中,A类表示“自己看过”,B类表示“听家长讲过”,
C类表示“听同学讲过”,D类表示“不知道”,划分类别后的数据整理如表:
类别 | A | B | C | D |
频数 | 30 | 40 | 24 | b |
频率 | a | 0.4 | 0.24 | 0.06 |
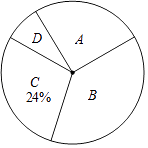
(1)表中的a=b=;
(2)根据表中数据,求扇形统计图中类别为B的学生数所对应的扇形圆心角的度数;
(3)若该校有学生1000名,根据调查结果估计该校学生中类别为C的人数约为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com