练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图，AB是圆O的弦，P是AB上一点，AB=10，OP=5，圆O的半径为7，求AP．
    考点：垂径定理,勾股定理
    专题：
    分析：首先过点O作OC⊥AB于点C，连接OA，由垂径定理即可求得AC的长，然后由勾股定理，求得OC与PC的长，继而求得答案．
    解答：解：过点O作OC⊥AB于点C，连接OA，
    ∵AB=10，
    ∴AC=
    1
    2
    AB=5，
    ∵OA=7，
    ∴OC=
    		OA2-AC2
    =2
    		6
    ，
    ∴PC=
    		OP2-OC2
    =
    		52-(2
    		6
    )2
    =1，
    ∴AP=AC+PC=6．
    点评：此题考查了垂径定理以及勾股定理．此题难度不大，注意掌握辅助线的作法，注意掌握数形结合思想的应用．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图，在△ABC中，AB=AC，∠BAC=90°，BC=8，⊙A与BC相切于点D，且与AB、AC分别交于点E、F，则劣弧
    EF
    的长是（　　）
    A、πB、2πC、3πD、4π

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图所示，图①，图②中∠B，∠E的两边均分别平行，即BC∥EF，AB∥DE，EF交与点O
    （1）请你通过观察，测量，分别写出图①②中∠B与∠E是怎样的大小关系？
    （2）说明（1）中所写关于图②结论的理由；
    （3）用语言叙述两边分别平行的两角之间的关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图为5×5的方格，其中有A、B、C三点，现有一点P在其它格点上，且A、B、C、P为轴对称图形，问共有几个这样的点P（　　）
    A、5B、4C、3D、2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知：如图△ABC中，BD和CE是三角形的高，M为BC的中点，P为DE的中点．求证：PM⊥DE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图所示，南北方向QP为我国的领海线，以西为公海，晚上10点28分，我边防反偷渡巡逻艇122号在A处发现其正西方向有一只可疑船只C之间的距离为10海里，A、B两艇之间的距离为6海里，B艇与可疑船只C之间的距离为8海里，若该可疑船只的速度为12.8海里/时，问该可疑船只最早在何时进入我国领海？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

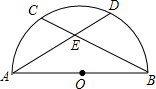    如图，已知：AB是⊙O的直径，C、D是弧
    AB
    的三等分点，连结BC、AD、BC与AD相交于点E．则∠AEB的度数是（　　）
    A、150°B、135°
    C、140°D、120°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （1）计算：（-
    		2
    2
    ）-1+（2-
    		2015
    ）0-|
    		8
    -3|；
    （2）计算：（
    5
    3
    +
    3
    5
    ）×
    		20
    -（
    		3
    +1）2；
    （3）解方程组：
    x-y=21①
    x+y=-1②

    （4）解方程组：
    2(x+1)=y+3①
    3(y-1)=x+4②
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    有一“数值转换机”如图所示，则输出的结果为（　　）
    A、x-
    2
    3
    B、
    x
    3
    -2
    C、
    x-2
    3
    D、
    2
    3

    查看答案和解析>>

    同步练习册答案