
【题目】如图,已知点E、F在四边形ABCD的对角线延长线上,AE=CF,DE∥BF,∠1=∠2.
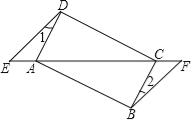
(1)求证:△AED≌△CFB;
(2)若AD⊥CD,四边形ABCD是什么特殊四边形?请说明理由.
【答案】(1)证明见解析
(2)四边形ABCD是矩形;理由见解析
【解析】
试题(1)根据两直线平行,内错角相等可得∠E=∠F,再利用“角角边”证明△AED和△CFB全等即可;
(2)根据全等三角形对应边相等可得AD=BC,∠DAE=∠BCF,再求出∠DAC=∠BCA,然后根据内错角相等,两直线平行可得AD∥BC,再根据一组对边平行且相等的四边形是平行四边形证明四边形ABCD是平行四边形,再根据有一个角是直角的平行四边形是矩形解答.
(1)证明:∵DE∥BF,
∴∠E=∠F,
在△AED和△CFB中,
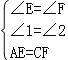 ,
,
∴△AED≌△CFB(AAS);
(2)解:四边形ABCD是矩形.
理由如下:∵△AED≌△CFB,
∴AD=BC,∠DAE=∠BCF,
∴∠DAC=∠BCA,
∴AD∥BC,
∴四边形ABCD是平行四边形,
又∵AD⊥CD,
∴四边形ABCD是矩形.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 的图像交
的图像交![]() 轴于
轴于![]() ,
,![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,连接
,连接![]() ,已知
,已知![]() .
.
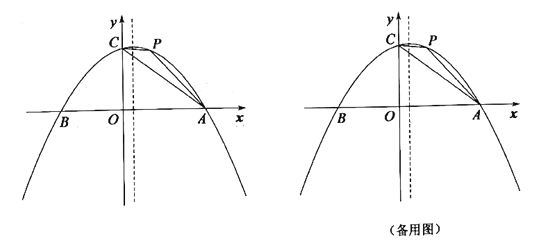
(1)点![]() 的坐标是______;
的坐标是______;
(2)若点![]() 是抛物线上的任意一点,连接
是抛物线上的任意一点,连接![]() 、
、![]() .
.
①当![]() 与
与![]() 的面积相等时,求点
的面积相等时,求点![]() 的坐标;
的坐标;
②把![]() 沿着
沿着![]() 翻折,若点
翻折,若点![]() 与抛物线对称轴上的点
与抛物线对称轴上的点![]() 重合,直接写出点
重合,直接写出点![]() 的横坐标.
的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标中,菱形ABCO的顶点O在坐标原点,且与反比例函数y=![]() 的图象相交于A(m,3
的图象相交于A(m,3![]() ),C两点,已知点B(2
),C两点,已知点B(2![]() ,2
,2![]() ),则k的值为( )
),则k的值为( )

A. 6B. ﹣6C. 6![]() D. ﹣6
D. ﹣6![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y1=ax2+bx+c(a>0)的图象与x轴交于A(﹣1,0),B(n,0)两点,一次函数y2=2x+b的图象过点A.
(1)若a=![]() .
.
①若二次函数y1=ax2+bx+c(a>0)与y轴交于点C,求△ABC的面积;
②设y3=y1﹣my2,是否存在正整数m,当x≥0时,y3随x的增大而增大?若存在,求出正整数m的值;若不存在,请说明理由.
(2)若![]() <a<
<a<![]() ,求证:﹣5<n<﹣4.
,求证:﹣5<n<﹣4.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙为两座建筑物,它们之间的水平距离BC为30m,在A点测得D点的仰角∠EAD为45°,在B点测得D点的仰角∠CBD为60°,则乙建筑物的高度为( )米.
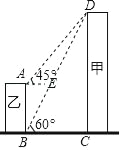
A. 30![]() B. 30
B. 30![]() ﹣30 C. 30 D. 30
﹣30 C. 30 D. 30![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,图①是一个三角形,分别连接三边中点得图②,再分别连接图②中的小三角形三边中点,得图③……按此方法继续下去.

在第![]() 个图形中有______个三角形(用含
个图形中有______个三角形(用含![]() 的式子表示)
的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
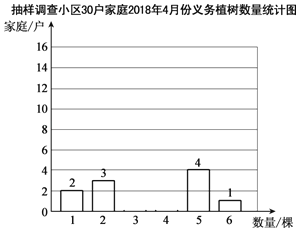
【题目】“绿水青山就是金山银山”,北京市民积极参与义务植树活动.小武同学为了了解自己小区300户家庭在2018年4月份义务植树的数量,进行了抽样调查,随即抽取了其中30户家庭,收集的数据如下(单位:棵):
1 1 2 3 2 3 2 3 3 4 3 3 4 3 3
5 3 4 3 4 4 5 4 5 3 4 3 4 5 6
(1)对以上数据进行整理、描述和
①绘制如下的统计图,请补充完整;
②这30户家庭2018年4月份义务植树数量的平均数是______,众数是______;
(2)“互联网+全民义务植树”是新时代首都全民义务植树组织形式和尽责方式的一大创新,2018年首次推出义务植树网上预约服务,小武同学所调查的这30户家庭中有7户家庭采用了网上预约义务植树这种方式,由此可以估计该小区采用这种形式的家庭有______户.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司推出一款产品,经市场调查发现,该产品的日销售量y(个)与销售单价x(元)之间满足一次函数关系.关于销售单价,日销售量,日销售利润的几组对应值如下表:
销售单价x(元) | 85 | 95 | 105 | 115 |
日销售量y(个) | 175 | 125 | 75 | m |
日销售利润w(元) | 875 | 1875 | 1875 | 875 |
(注:日销售利润=日销售量×(销售单价﹣成本单价))
(1)求y关于x的函数解析式(不要求写出x的取值范围)及m的值;
(2)根据以上信息,填空:
该产品的成本单价是 元,当销售单价x= 元时,日销售利润w最大,最大值是 元;
(3)公司计划开展科技创新,以降低该产品的成本,预计在今后的销售中,日销售量与销售单价仍存在(1)中的关系.若想实现销售单价为90元时,日销售利润不低于3750元的销售目标,该产品的成本单价应不超过多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com